Manual
Introduction
The Open Dynamics Engine (ODE) is a free, industrial quality library for simulating articulated rigid body dynamics. Proven applications include simulating ground vehicles, legged creatures, and moving objects in VR environments. It is fast, flexible and robust, and has built-in collision detection. ODE is being developed by Russell Smith with help from several contributors.
If rigid body simulation does not make much sense to you, check out What is a Physics SDK?.
Features
ODE is good for simulating articulated rigid body structures. An articulated structure is created when rigid bodies of various shapes are connected together with joints of various kinds. Examples are ground vehicles (where the wheels are connected to the chassis), legged creatures (where the legs are connected to the body), or stacks of objects.
ODE is designed to be used in interactive or real-time simulation. It is particularly good for simulating moving objects in changeable virtual reality environments. This is because it is fast, robust and stable, and the user has complete freedom to change the structure of the system even while the simulation is running.
ODE uses a highly stable integrator, so that the simulation errors should not grow out of control. The physical meaning of this is that the simulated system should not "explode" for no reason (believe me, this happens a lot with other simulators if you are not careful). ODE emphasizes speed and stability over physical accuracy.
ODE has hard contacts. This means that a special non-penetration constraint is used whenever two bodies collide. The alternative, used in many other simulators, is to use virtual springs to represent contacts. This is difficult to do right and extremely error-prone.
ODE has a built-in collision detection system. However you can ignore it and do your own collision detection if you want to. The current collision primitives are sphere, box, cylinder, capsule, plane, ray, and triangular mesh - more collision objects will come later. ODE's collision system provides fast identification of potentially intersecting objects, through the concept of "spaces". (See the Collision Matrix to find out which primives --- primitive collision are implemented)
Here are the features:
- Rigid bodies with arbitrary mass distribution.
- Joint types: ball-and-socket, hinge, slider (prismatic), hinge-2, fixed, angular motor, linear motor, universal.
- Collision primitives: sphere, box, cylinder, capsule, plane, ray, and triangular mesh, convex.
- Collision spaces: Quad tree, hash space, and simple.
- Simulation method: The equations of motion are derived from a Lagrange multiplier velocity based model due to Trinkle/Stewart and Anitescu/Potra.
- A first order integrator is being used. It's fast, but not accurate enough for quantitative engineering yet. Higher order integrators will come later.
- Choice of time stepping methods: either the standard ``big matrix'' method or the newer iterative QuickStep method can be used.
- Contact and friction model: This is based on the Dantzig LCP solver described by Baraff, although ODE implements a faster approximation to the Coloumb friction model.
- Has a native C interface (even though ODE is mostly written in C++).
- Has a C++ interface built on top of the C one.
- Many unit tests, and more being written all the time.
- Platform specific optimizations.
ODE's License
ODE is Copyright © 2001-2004 Russell L. Smith. All rights reserved.
This library is free software; you can redistribute it and/or modify it under the terms of EITHER:
- The GNU Lesser General Public License as published by the Free Software Foundation; either version 2.1 of the License, or (at your option) any later version. The text of the GNU Lesser General Public License is included with this library in the file
LICENSE.TXT. - The BSD-style license that is included with this library in the file
LICENSE-BSD.TXT.
This library is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the files LICENSE.TXT and LICENSE-BSD.TXT for more details.
The ODE Community
Do you have questions or comments about ODE? Think you can help? Please write to the ODE mailing list.
Install and Use
Getting the Source Code
ODE is currently distributed in source code form only; there are no pre-built binary packages available. Because of the many different ways in which ODE can be configured it is considered best practice to start with the source code and create a build tailored to your particular project. For the same reason, Linux distributions are discouraged from trying to develop a "canonical" binary version.
Stable releases are available from the the SourceForge.net project page.
A Subversion repository is also available on SourceForge.
If you have any questions, there is a very helpful mailing list. If you plan on using ODE you should definitely sign up. The list is fairly low traffic, high signal-to-noise, and extremely useful. You might also want to search the archive of the old mailing list.
Before You Build
Before you start, you should know that there are two parts to ODE. There is "ODE", which is the physics and collision detection library. Then there is "DrawStuff", a simple wrapper over Win32/X11 and OpenGL which is used for the demo applications. This often causes confusion: DrawStuff is a simple library written only to display the ODE demos and is not intended to be used in your own projects. DrawStuff requires OpenGL, and X11 on Mac OS X; ODE does not. You do not have to build DrawStuff or the demo applications in order to use ODE.
Due to the wide variety of platforms, environments, and tools used by the ODE community, two different build approaches are provided. If the sequence ./configure; make; make install is your preferred approach (*nix and Mac OS X, primarily), see Building with Automake below. If you prefer an IDE, see Building with Premake, farther down.
Building with Automake
If you downloaded the source code from Subversion, bootstrap autotools by running the autogen.sh script. If you downloaded a stable release package this has already been done for you.
$ sh autogen.sh
Note that you need to have a recent autoconf (2.61), automake (1.10) and libtool. You may see some "underquoted definition" warnings depending on your platform, these are (for now) harmless warnings regarding scripts from other m4 installed packages.
Next, configure the build by running the command:
$ ./configure
By default this will set up ODE to build a static library with single precision math, trimesh support, and debug symbols enabled. You can modify this default configuration by supplying options to the configure command. Type the command
$ ./configure --help
...for a full list of available options. Here are a few of the most important ones:
- --disable-demos --without-x to let it compile on Mac OS X
- --enable-double-precision enables double precision math
- --with-trimesh=opcode use OPCODE trimesh support (default)
- --with-trimesh=gimpact use GIMPACT trimesh support
- --with-trimesh=none disable trimesh support
Once configure has run successfully, you can build ODE with:
$ make $ sudo make install
The latter command will also enable pkg-config support by installing the ode-config and ode.pc scripts. To build your programs with pkg-config, add (including the backticks):
`pkg-config ode --cflags`
to your compiler flags (CFLAGS or CXXFLAGS), and
`pkg-config ode --libs`
to your linker flags (LDFLAGS). This pair of commands will set all of the appropriate compiler and linker flags, based on the ODE configuration. If used inside a Makefile, you can use the $(shell) function instead of the backticks because it is more portable.
MinGW/MSYS users will need to install some appropriate packages such as autoconf, automake and libtool, as well as pkg-config (not provided by the MinGW folks, but by the GTK+ project), in order to run autogen.sh. Like in *nix systems, avoid building ODE in directories with spaces. If you don't already have a working MSYS setup, the Premake build instructions below will be much more helpful.
Building with Premake
Premake is a build configuration tool which generates customized project files for Visual Studio, Code::Blocks, CodeLite, and GNU Make (XCode support is coming). The ODE source code includes a Windows version of the Premake executable at build/premake4.exe; users of other platforms can download a source or binary package.
To generate the project files you will need to run Premake in the ode/build directory and specify your toolset of choice (Premake is a command-line program and must be run from a console or terminal). For instance, this will generate files for Visual Studio 2008:
$ cd ode/build $ premake4 vs2008
The generated project files (.sln, .vcproj) will be placed in an appropriately named subdirectory, in this case ode/build/vs2008.
For a complete list of supported toolsets and options, type:
$ premake4 --help
Several configuration options are available, the most notable include:
- --with-demos
- includes the demo applications and Drawstuff library.
- --with-tests
- includes the automated test suite, recommended if you intend to modify ODE.
- --no-trimesh
- excludes support for triangle mesh collision geometries, reducing the size of the library.
- --with-gimpact
- uses the GIMPACT library to check for triangle mesh collisions instead of OPCODE.
- --with-libccd
- uses libccd to handle pairs of geoms that don't have yet specialized tests.
Specify options before the toolset when running Premake, like so:
$ premake4 --with-demos --with-tests vs2008
The generated project files provide several different possible build configurations, including use of single or double precision numbers, and static or shared libraries. If you used Premake to generate GNU makefiles, see the comments at the start of Makefile for instructions on selecting a configuration when building. IDE users can set the build configuration as they normally would.
Premake has recently added experimental support for cross-compiling "platforms", enabling it to target the Xbox 360, Playstation 3, and (not really cross-compiling, but still) Mac OS X universal binaries.
You can see a complete list of available platforms in Premake's help.
Rather than cluttering up the default project files with a ton of platform combinations that most people won't use, I'd suggest that people who want to target these platforms generate their own project files, using the --platform argument to add support for their preferred targets.
$ premake4 --platform=ps3 vs2008
Install with Python bindings
Open Dynamics Engine can be used in Python software (does not matter if it is a simple script or a complex library) through the included bindings, which must be compiled for each platform.
These bindings are based in project PyODE, which is obsolete (as of 2013-01-21, its latest release dates from 2010-03-22), by Ethan Glasser-Camp and others. The work to bring them up to date, replace Pyrex with Cython and integrate them into the official ODE source code was done by Gideon Klompje.
Warning: The Python bindings are far more recent and less popular than ODE itself thus they probably have more bugs.
Linux
The complete process to compile and install an ODE release (more steps are needed for repository snapshots) with Python bindings is:
- tar xf ode-0.12.tar.gz
- cd ode-0.12
- ./configure --enable-double-precision --with-trimesh=opcode --enable-new-trimesh --enable-shared
- make
- make install
- cd bindings/python/
- python setup.py install
(you may need to prepend sudo to make install and python setup.py install depending on your OS user's privileges)
(These instructions have been tested in Ubuntu 12.04 64-bits and Debian 7 64-bits)
Windows
Thanks to Christoph Gohlke there are available graphical installers for Windows (both 32 an 64 bits), Python versions 2.6, 2.7, 3.2 and 3.3. You can find them at his website Unofficial Windows Binaries for Python Extension Packages (if it's down, check here).
Uninstall
With make
To uninstall ODE (say, version 0.12), you must perform the same steps you did when installing, until before compiling. Then uninstall using make.
These are example steps. Replace the configure arguments with the ones you used in your installation.
tar xf ode-0.12.tar.gzcd ode-0.12./configure --enable-double-precision --with-trimesh=opcode --enable-new-trimesh --enable-sharedmake uninstall
(you may need to prepend sudo to the last command depending on your OS user's privileges)
Using ODE
The best way to understand how to use ODE is to look at the supplied test/example programs, located in ode/ode/demo.
To create an application using ODE, follow these steps:
- Add
ode/includeto your list of include file paths. #include <ode/ode.h>- Look in
ode/liband add the appropriate library search path and file name, depending on which build configuration was used. For instance,ode/lib/DebugSingleDLLandode_singled.lib. - Add one of the preprocessor symbols
dSINGLE(single precision) ordDOUBLE(double precision), depending on how ODE was configured. If none is defined, single precision is assumed; if the wrong precision is enabled all floating-point data going in and out of ODE will be corrupt, producing all kinds of errors.
When ODE is used with the dWorldStep function, heavy use is made of the stack for storing temporary values. For very large systems several megabytes of stack can be used. If you experience unexplained out-of-memory errors or data corruption, especially on Windows, try increasing the stack size, or switching to dWorldQuickStep.
Concepts
Background
Here is where I will write some background information about rigid body dynamics and simulation. But in the meantime, please refer to Baraff's excellent SIGGRAPH tutorial.
Rigid bodies
A rigid body has various properties from the point of view of the simulation. Some properties change over time:
- Position vector (x,y,z) of the body's point of reference. Currently the point of reference must correspond to the body's center of mass.
- Linear velocity of the point of reference, a vector (vx,vy,vz).
- Orientation of a body, represented by a quaternion (qs,qx,qy,qz) or a 3x3 rotation matrix.
- Angular velocity vector (wx,wy,wz) which describes how the orientation changes over time.
Other body properties are usually constant over time:
- Mass of the body.
- Position of the center of mass with respect to the point of reference. In the current implementation the center of mass and the point of reference must coincide.
- Inertia matrix. This is a 3x3 matrix that describes how the body's mass is distributed around the center of mass. Conceptually each body has an x-y-z coordinate frame embedded in it, that moves and rotates with the body, as shown in figure 1.
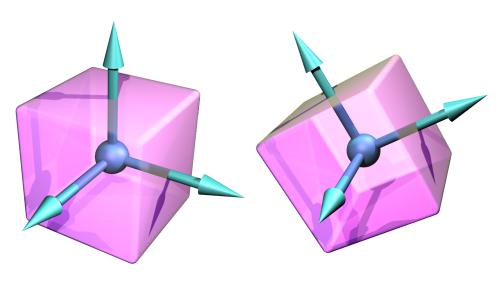
Figure 1: The body coordinate frame.
The origin of this coordinate frame is the body's point of reference. Some values in ODE (vectors, matrices etc) are relative to the body coordinate frame, and others are relative to the global coordinate frame.
Note that the shape of a rigid body is not a dynamical property (except insofar as it influences the various mass properties). It is only collision detection that cares about the detailed shape of the body.
Islands and Disabled Bodies
Bodies are connected to each other with joints. An "island" of bodies is a group that can not be pulled apart - in other words each body is connected somehow to every other body in the island.
Each island in the world is treated separately when the simulation step is taken. This is useful to know: if there are N similar islands in the simulation then the step computation time will be O(N).
Each body can be enabled or disabled. Disabled bodies are effectively "turned off" and are not updated during a simulation step. Disabling bodies is an effective way to save computation time when it is known that the bodies are motionless or otherwise irrelevant to the simulation.
If there are any enabled bodies in an island then every body in the island will be enabled at the next simulation step. Thus to effectively disable an island of bodies, every body in the island must be disabled. If a disabled island is touched by another enabled body then the entire island will be enabled, as a contact joint will join the enabled body to the island.
Integration
The process of simulating the rigid body system through time is called integration. Each integration step advances the current time by a given step size, adjusting the state of all the rigid bodies for the new time value. There are two main issues to consider when working with any integrator:
- How accurate is it? That is, how closely does the behavior of the simulated system match what would happen in real life?
- How stable is it? That is, will calculation errors ever cause completely non-physical behavior of the simulated system? (e.g. causing the system to "explode" for no reason).
ODE's current integrator is very stable, but not particularly accurate unless the step size is small. For most uses of ODE this is not a problem -- ODE's behavior still looks perfectly physical in almost all cases. However ODE should not be used for quantitative engineering until this accuracy issue has been addressed in a future release.
Force accumulators
Between each integrator step the user can call functions to apply forces to the rigid body. These forces are added to "force accumulators" in the rigid body object. When the next integrator step happens, the sum of all the applied forces will be used to push the body around. The forces accumulators are set to zero after each integrator step.
Joints and constraints
In real life a joint is something like a hinge, that is used to connect two objects. In ODE a joint is very similar: It is a relationship that is enforced between two bodies so that they can only have certain positions and orientations relative to each other. This relationship is called a constraint -- the words joint and constraint are often used interchangeably. Figure 2 shows three different constraint types.

Figure 2: Three different constraint types.
The first is a ball and socket joint that constraints the ``ball of one body to be in the same location as the "socket" of another body. The second is a hinge joint that constraints the two parts of the hinge to be in the same location and to line up along the hinge axle. The third is a slider joint that constraints the "piston" and "socket" to line up, and additionally constraints the two bodies to have the same orientation.
Each time the integrator takes a step all the joints are allowed to apply constraint forces to the bodies they affect. These forces are calculated such that the bodies move in such a way to preserve all the joint relationships.
Each joint has a number of parameters controlling its geometry. An example is the position of the ball-and-socket point for a ball-and-socket joint. The functions to set joint parameters all take global coordinates, not body-relative coordinates. A consequence of this is that the rigid bodies that a joint connects must be positioned correctly before the joint is attached.
Joint groups
A joint group is a special container that holds joints in a world. Joints can be added to a group, and then when those joints are no longer needed the entire group of joints can be very quickly destroyed with one function call. However, individual joints in a group can not be destroyed before the entire group is emptied.
This is most useful with contact joints, which are added and remove from the world in groups every time step.
Joint error and the Error Reduction Parameter (ERP)
When a joint attaches two bodies, those bodies are required to have certain positions and orientations relative to each other. However, it is possible for the bodies to be in positions where the joint constraints are not met. This "joint error" can happen in two ways:
- If the user sets the position/orientation of one body without correctly setting the position/orientation of the other body.
- During the simulation, errors can creep in that result in the bodies drifting away from their required positions.
Figure 3 shows an example of error in a ball and socket joint (where the ball and socket do not line up).
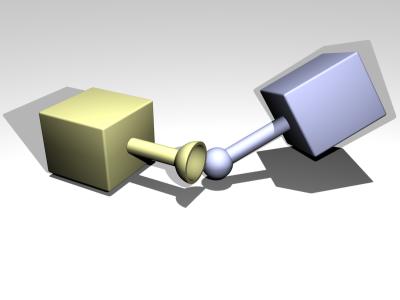
Figure 3: An example of error in a ball and socket joint.
There is a mechanism to reduce joint error: during each simulation step each joint applies a special force to bring its bodies back into correct alignment. This force is controlled by the error reduction parameter (ERP), which has a value between 0 and 1.
The ERP specifies what proportion of the joint error will be fixed during the next simulation step. If ERP=0 then no correcting force is applied and the bodies will eventually drift apart as the simulation proceeds. If ERP=1 then the simulation will attempt to fix all joint error during the next time step. However, setting ERP=1 is not recommended, as the joint error will not be completely fixed due to various internal approximations. A value of ERP=0.1 to 0.8 is recommended (0.2 is the default).
A global ERP value can be set that affects most joints in the simulation. However some joints have local ERP values that control various aspects of the joint.
Soft constraint and Constraint Force Mixing (CFM)
Most constraints are by nature "hard". This means that the constraints represent conditions that are never violated. For example, the ball must always be in the socket, and the two parts of the hinge must always be lined up. In practice constraints can be violated by unintentional introduction of errors into the system, but the error reduction parameter can be set to correct these errors.
Not all constraints are hard. Some "soft" constraints are designed to be violated. For example, the contact constraint that prevents colliding objects from penetrating is hard by default, so it acts as though the colliding surfaces are made of steel. But it can be made into a soft constraint to simulate softer materials, thereby allowing some natural penetration of the two objects when they are forced together.
There are two parameters that control the distinction between hard and soft constraints. The first is the error reduction parameter (ERP) that has already been introduced. The second is the constraint force mixing (CFM) value, that is described below.
Constraint Force Mixing (CFM)
What follows is a somewhat technical description of the meaning of CFM. If you just want to know how it is used in practice then skip to the next section.
Traditionally the constraint equation for every joint has the form
- [math]\displaystyle{ \mathbf{J} v = \mathbf{c} }[/math]
where [math]\displaystyle{ v }[/math] is a velocity vector for the bodies involved, [math]\displaystyle{ \mathbf{J} }[/math] is a "Jacobian" matrix with one row for every degree of freedom the joint removes from the system, and [math]\displaystyle{ \mathbf{c} }[/math] is a right hand side vector. At the next time step, a vector [math]\displaystyle{ \lambda }[/math] is calculated (of the same size as [math]\displaystyle{ \mathbf{c} }[/math]) such that the forces applied to the bodies to preserve the joint constraint are:
- [math]\displaystyle{ F_c = \mathbf{J}^T \lambda }[/math]
ODE adds a new twist. ODE's constraint equation has the form
- [math]\displaystyle{ \mathbf{J} v = \mathbf{c} + \textbf{CFM} \, \lambda }[/math]
where CFM is a square diagonal matrix. CFM mixes the resulting constraint force in with the constraint that produces it. A nonzero (positive) value of CFM allows the original constraint equation to be violated by an amount proportional to CFM times the restoring force [math]\displaystyle{ \lambda }[/math] that is needed to enforce the constraint. Solving for [math]\displaystyle{ \lambda }[/math] gives
- [math]\displaystyle{ (\mathbf{J} \mathbf{M}^{-1} \mathbf{J}^T + \frac{1}{h} \textbf{CFM}) \lambda = \frac{1}{h} \mathbf{c} }[/math]
Thus CFM simply adds to the diagonal of the original system matrix. Using a positive value of CFM has the additional benefit of taking the system away from any singularity and thus improving the factorizer accuracy.
How To Use ERP and CFM
ERP and CFM can be independently set in many joints. They can be set in contact joints, in joint limits and various other places, to control the spongyness and springyness of the joint (or joint limit).
If CFM is set to zero, the constraint will be hard. If CFM is set to a positive value, it will be possible to violate the constraint by "pushing on it" (for example, for contact constraints by forcing the two contacting objects together). In other words the constraint will be soft, and the softness will increase as CFM increases. What is actually happening here is that the constraint is allowed to be violated by an amount proportional to CFM times the restoring force that is needed to enforce the constraint. Note that setting CFM to a negative value can have undesirable bad effects, such as instability. Don't do it.
By adjusting the values of ERP and CFM, you can achieve various effects. For example you can simulate springy constraints, where the two bodies oscillate as though connected by springs. Or you can simulate more spongy constraints, without the oscillation. In fact, ERP and CFM can be selected to have the same effect as any desired spring and damper constants. If you have a spring constant [math]\displaystyle{ k_p }[/math] and damping constant [math]\displaystyle{ k_d }[/math], then the corresponding ODE constants are:
- [math]\displaystyle{ ERP = \frac{h k_p} {h k_p + k_d} \quad \quad CFM = \frac{1} {h k_p + k_d} }[/math]
where [math]\displaystyle{ h }[/math] is the step size. These values will give the same effect as a spring-and-damper system simulated with implicit first order integration.
Increasing CFM, especially the global CFM, can reduce the numerical errors in the simulation. If the system is near-singular, then this can markedly increase stability. In fact, if the system is mis-behaving, one of the first things to try is to increase the global CFM.
Collision handling
There is a lot that needs to be written about collision handling.
Collisions between bodies or between bodies and the static environment are handled as follows:
- Before each simulation step, the user calls collision detection functions to determine what is touching what. These functions return a list of contact points. Each contact point specifies a position in space, a surface normal vector, and a penetration depth.
- A special contact joint is created for each contact point. The contact joint is given extra information about the contact, for example the friction present at the contact surface, how bouncy or soft it is, and various other properties.
- The contact joints are put in a joint "group", which allows them to be added to and removed from the system very quickly. The simulation speed goes down as the number of contacts goes up, so various strategies can be used to limit the number of contact points.
- A simulation step is taken.
- All contact joints are removed from the system.
Note that the built-in collision functions do not have to be used - other collision detection libraries can be used as long as they provide the right kinds of contact point information.
Typical simulation code
A typical simulation will proceed like this:
- Create a dynamics world.
- Create bodies in the dynamics world.
- Set the state (position etc) of all bodies.
- Create joints in the dynamics world.
- Attach the joints to the bodies.
- Set the parameters of all joints.
- Create a collision world and collision geometry objects, as necessary.
- Create a joint group to hold the contact joints.
- Loop:
- Apply forces to the bodies as necessary.
- Adjust the joint parameters as necessary.
- Call collision detection.
- Create a contact joint for every collision point, and put it in the contact joint group.
- Take a simulation step.
- Remove all joints in the contact joint group.
- Destroy the dynamics and collision worlds.
Physics model
The various methods and approximations that are used in ODE are discussed here.
Friction Approximation
We really need more pictures here.
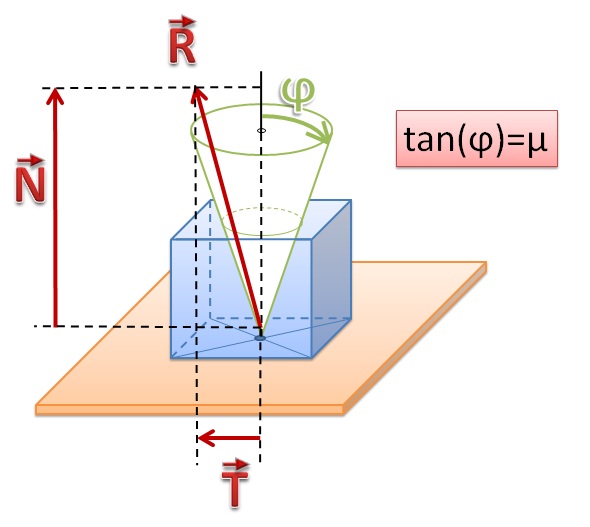
Figure: Angle of friction.
The Coulomb friction model is a simple, but effective way to model friction at contact points. It is a simple relationship between the normal and tangential forces present at a contact point (see the contact joint section for a description of these forces). The rule is:
- [math]\displaystyle{ | F_\mathrm{T} | \leq \mu | F_\mathrm{N} | }[/math]
where [math]\displaystyle{ F_\mathrm{T} }[/math] and [math]\displaystyle{ F_\mathrm{N} }[/math] are the normal and tangential force vectors respectively, and [math]\displaystyle{ \mu }[/math] is the friction coefficient (typically a number around 1.0). This equation defines a "friction cone" - imagine a cone with [math]\displaystyle{ F_N }[/math] as the axis and the contact point as the vertex. If the total friction force vector is within the cone then the contact is in "sticking mode", and the friction force is enough to prevent the contacting surfaces from moving with respect to each other. If the force vector is on the surface of the cone then the contact is in "sliding mode", and the friction force is typically not large enough to prevent the contacting surfaces from sliding. The parameter [math]\displaystyle{ \mu }[/math] thus specifies the maximum ratio of tangential to normal force.
ODE's friction models are approximations to the friction cone, for reasons of efficiency. There are currently two approximations to chose from:
- The meaning of [math]\displaystyle{ \mu }[/math] is changed so that it specifies the maximum friction (tangential) force that can be present at a contact, in either of the tangential friction directions. This is rather non physical because it is independent of the normal force, but it can be useful and it is the computationally cheapest option. Note that in this case [math]\displaystyle{ \mu }[/math] is a force limit and must be chosen appropriate to the simulation.
- The friction cone is approximated by a friction pyramid aligned with the first and second friction directions (I really need a picture here). A further approximation is made: first ODE computes the normal forces assuming that all the contacts are frictionless. Then it computes the maximum limits [math]\displaystyle{ F_\mathrm{m} }[/math] for the friction (tangential) forces from
- [math]\displaystyle{ F_\mathrm{m} = \mu | F_\mathrm{N} | }[/math]
and then proceeds to solve for the entire system with these fixed limits (in a manner similar to approximation 1 above). This differs from a true friction pyramid in that the "effective" mu is not quite fixed. This approximation is easier to use as [math]\displaystyle{ \mu }[/math] is a unit-less ratio the same as the normal Coloumb friction coefficient, and thus can be set to a constant value around 1.0 without regard for the specific simulation.
Data Types and Conventions
The basic data types
The ODE library can be built to use either single or double precision floating point numbers. Single precision is faster and uses less memory, but the simulation will have more numerical error that can result in visible problems. You will get less accuracy and stability with single precision.
(must describe what factors influence accuracy and stability).
The floating point data type is dReal. Other commonly used types are dVector3, dMatrix3, dQuaternion.
The non-scalar floating point types are all implemented as simple arrays of dReals. Their layout conventions are as follows:
| Name | Implementation | Format |
|---|---|---|
dQuaternion
|
dReal[4] | [ w, x, y, z ], where w is the real part and (x, y, z) form the vector part. |
dVector4
|
dReal[4] | [ x, y, z, 1.0 ] |
dVector3
|
dReal[4] | Same as dVector4; the 4th element is there only for better alignment, and should be ignored.
|
dMatrix4
|
dReal[4*4] | A 4x4 matrix, laid out in row-major order, usually used as a homogeneous transform matrix. This means that the upper-left 3x3 elements are a rotation matrix, the first three elements of the last column are a translation vector, and the last row is simply [ 0, 0, 0, 1 ]. |
dMatrix3
|
dReal[3*4] | A 3x3 matrix with the elements laid out in row-major order. The last column is ignored and, as dVector3, is used only for better alignment. |
Objects and IDs
There are various kinds of object that can be created:
- dWorld - a dynamics world, that contains all the simulation data.
- dBody - a rigid body; it does not have any shape: it needs one or more dGeoms for that.
- dJoint - a joint.
- dJointGroup - a group of joints, makes it easy to destroy all joints at once.
- dSpace - a collision space, used to organize and speed up collision tests.
- dGeom - a shape used to detect collisions.
Functions that deal with these objects take and return object IDs. The object ID types are dWorldID, dBodyID, etc.
Argument conventions
All 3-vectors (x,y,z) supplied to "set" functions are given as individual x,y,z arguments.
All 3-vector result arguments to "get" function are pointers to arrays of dReal.
Larger vectors are always supplied and returned as pointers to arrays of dReal.
All coordinates are in the global frame except where otherwise specified.
C versus C++
The ODE library is written in C++, but its public interface is made of simple C functions, not classes. Why is this?
- Using a C interface only is simpler - the features of C++ do not help much for ODE.
- It prevents C++ mangling and runtime-support problems across multiple compilers.
- The user doesn't have to be familiar with C++ quirks to use ODE.
There's a semi-official C++ wrapper distributed with the library, in the odecpp*.h headers, but it has some design limitations.
Debugging
The ODE library can be compiled in "debugging" or "release" mode. Debugging mode is slower, but function arguments are checked and many run-time tests are done to ensure internal consistency. Release mode is faster, but no checking is done.
World
General Functions
The world object is a container for rigid bodies and joints. Objects in different worlds can not interact, for example rigid bodies from two different worlds can not collide.
All the objects in a world exist at the same point in time, thus one reason to use separate worlds is to simulate systems at different rates.
Most applications will only need one world.
dWorldID dWorldCreate();
Create a new, empty world and return its ID number.
void dWorldDestroy (dWorldID);
Destroy a world and everything in it. This includes all bodies, and all joints that are not part of a joint group. Joints that are part of a joint group will be deactivated, and can be destroyed by calling, for example, dJointGroupEmpty.
void dWorldSetGravity (dWorldID, dReal x, dReal y, dReal z); void dWorldGetGravity (dWorldID, dVector3 gravity);
Set and get the world's global gravity vector. In the SI units the Earth's gravity vector would be (0,0,-9.81), assuming that +z is up. The default is no gravity, i.e. (0,0,0).
void dWorldSetERP (dWorldID, dReal erp); dReal dWorldGetERP (dWorldID);
Set and get the global ERP value, that controls how much error correction is performed in each time step. Typical values are in the range 0.1-0.8. The default is 0.2.
void dWorldSetCFM (dWorldID, dReal cfm); dReal dWorldGetCFM (dWorldID);
Set and get the global CFM (constraint force mixing) value. Typical values are in the range 10-9 -- 1. The default is 10-5 if single precision is being used, or 10-10 if double precision is being used.
void dWorldSetAutoDisableFlag (dWorldID, int do_auto_disable); int dWorldGetAutoDisableFlag (dWorldID); void dWorldSetAutoDisableLinearThreshold (dWorldID, dReal linear_threshold); dReal dWorldGetAutoDisableLinearThreshold (dWorldID); void dWorldSetAutoDisableAngularThreshold (dWorldID, dReal angular_threshold); dReal dWorldGetAutoDisableAngularThreshold (dWorldID); void dWorldSetAutoDisableSteps (dWorldID, int steps); int dWorldGetAutoDisableSteps (dWorldID); void dWorldSetAutoDisableTime (dWorldID, dReal time); dReal dWorldGetAutoDisableTime (dWorldID);
Set and get the default auto-disable parameters for newly created bodies. See the Rigid Body documentation on auto-disabling for a description of this feature. The default parameters are:
- AutoDisableFlag = disabled
- AutoDisableLinearThreshold = 0.01
- AutoDisableAngularThreshold = 0.01
- AutoDisableSteps = 10
- AutoDisableTime = 0
void dWorldImpulseToForce (dWorldID, dReal stepsize, dReal ix, dReal iy, dReal iz, dVector3 force);
If you want to apply a linear or angular impulse to a rigid body, instead of a force or a torque, then you can use this function to convert the desired impulse into a force/torque vector before calling the dBodyAdd... function.
This function is given the desired impulse as (ix,iy,iz) and puts the force vector in force. The current algorithm simply scales the impulse by 1/stepsize, where stepsize is the step size for the next step that will be taken.
This function is given a dWorldID because, in the future, the force computation may depend on integrator parameters that are set as properties of the world.
Stepping Functions
void dWorldStep (dWorldID, dReal stepsize);
Step the world. This uses a "big matrix" method that takes time on the order of m3 and memory on the order of m2, where m is the total number of constraint rows.
For large systems this will use a lot of memory and can be very slow, but this is currently the most accurate method.
void dWorldQuickStep (dWorldID, dReal stepsize);
Step the world. This uses an iterative method that takes time on the order of m*N and memory on the order of m, where m is the total number of constraint rows and N is the number of iterations.
For large systems this is a lot faster than dWorldStep, but it is less accurate.
QuickStep is great for stacks of objects especially when the auto-disable feature is used as well. However, it has poor accuracy for near-singular systems. Near-singular systems can occur when using high-friction contacts, motors, or certain articulated structures. For example, a robot with multiple legs sitting on the ground may be near-singular.
There are ways to help overcome QuickStep's inaccuracy problems:
- Increase CFM.
- Reduce the number of contacts in your system (e.g. use the minimum number of contacts for the feet of a robot or creature).
- Don't use excessive friction in the contacts.
- Use contact slip if appropriate
- Avoid kinematic loops (however, kinematic loops are inevitable in legged creatures).
- Don't use excessive motor strength.
- Use force-based motors instead of velocity-based motors.
Increasing the number of QuickStep iterations may help a little bit, but it is not going to help much if your system is really near singular.
void dWorldSetQuickStepNumIterations (dWorldID, int num); int dWorldGetQuickStepNumIterations (dWorldID);
Set and get the number of iterations that the QuickStep method performs per step. More iterations will give a more accurate solution, but will take longer to compute. The default is 20 iterations.
void dWorldSetQuickStepW (WorldID, dReal over_relaxation); dReal dWorldGetQuickStepW (dWorldID);
Set and get the over-relaxation parameter for QuickStep's Successive over relaxation algorithm. Default value is 1.3.
Variable Step Size: Don't!
Stepsize should be constant in your application. A variable stepsize is a one-way trip to a headache. For example, think of an object "resting" on the ground. It'll actually stabilize at a small depth into the ground. When step sizes vary, the ideal stable position will change at each step, and thus the object will jitter (and may very well gain energy!)
ODE was designed with fixed step-sizes in mind. It is possible to use variable step-sizes in ODE, but it isn't easy (and this editor can't help you).
Damping
See the Rigid Body damping documentation for more details.
dReal dWorldGetLinearDamping (dWorldID); dReal dWorldGetAngularDamping (dWorldID); void dWorldSetLinearDamping (dWorldID, dReal scale); void dWorldSetAngularDamping (dWorldID, dReal scale); void dWorldSetDamping (dWorldID, dReal linear_scale, dReal angular_scale); dReal dWorldGetLinearDampingThreshold (dWorldID); dReal dWorldGetAngularDampingThreshold (dWorldID); void dWorldSetLinearDampingThreshold (dWorldID, dReal threshold); void dWorldSetAngularDampingThreshold (dWorldID, dReal threshold);
Set/Get the world's default damping parameters (bodies will use the world's parameters by default). The default threshold is 0.01, and the default damping is zero (no damping).
dReal dWorldGetMaxAngularSpeed (dWorldID); void dWorldSetMaxAngularSpeed (dWorldID, dReal max_speed);
Set/Get the default maximum angular speed for new bodies.
Contact Parameters
void dWorldSetContactMaxCorrectingVel (dWorldID, dReal vel); dReal dWorldGetContactMaxCorrectingVel (dWorldID);
Set and get the maximum correcting velocity that contacts are allowed to generate. The default value is infinity (i.e. no limit). Reducing this value can help prevent "popping" of deeply embedded objects.
void dWorldSetContactSurfaceLayer (dWorldID, dReal depth); dReal dWorldGetContactSurfaceLayer (dWorldID);
Set and get the depth of the surface layer around all geometry objects. Contacts are allowed to sink into the surface layer up to the given depth before coming to rest. The default value is zero. Increasing this to some small value (e.g. 0.001) can help prevent jittering problems due to contacts being repeatedly made and broken.
Rigid Body Functions
Creating and Destroying Bodies
dBodyID dBodyCreate (dWorldID);
Create a body in the given world with default mass parameters at position (0,0,0). Return its ID.
void dBodyDestroy (dBodyID);
Destroy a body. All joints that are attached to this body will be put into limbo (i.e. unattached and not affecting the simulation, but they will NOT be deleted).
Position and orientation
void dBodySetPosition (dBodyID, dReal x, dReal y, dReal z); void dBodySetRotation (dBodyID, const dMatrix3 R); void dBodySetQuaternion (dBodyID, const dQuaternion q); void dBodySetLinearVel (dBodyID, dReal x, dReal y, dReal z); void dBodySetAngularVel (dBodyID, dReal x, dReal y, dReal z); const dReal * dBodyGetPosition (dBodyID); const dReal * dBodyGetRotation (dBodyID); const dReal * dBodyGetQuaternion (dBodyID); const dReal * dBodyGetLinearVel (dBodyID); const dReal * dBodyGetAngularVel (dBodyID);
These functions set and get the position, rotation, linear and angular velocity of the body. After setting a group of bodies, the outcome of the simulation is undefined if the new configuration is inconsistent with the joints/constraints that are present. When getting, the returned values are pointers to internal data structures, so the vectors are valid until any changes are made to the rigid body system structure.
dBodyGetRotation() returns a 4x3 rotation matrix.
Mass and force
void dBodySetMass (dBodyID, const dMass *mass); void dBodyGetMass (dBodyID, dMass *mass);
Set/get the mass of the body (see the mass functions).
void dBodyAddForce (dBodyID, dReal fx, dReal fy, dReal fz); void dBodyAddTorque (dBodyID, dReal fx, dReal fy, dReal fz); void dBodyAddRelForce (dBodyID, dReal fx, dReal fy, dReal fz); void dBodyAddRelTorque (dBodyID, dReal fx, dReal fy, dReal fz); void dBodyAddForceAtPos (dBodyID, dReal fx, dReal fy, dReal fz, dReal px, dReal py, dReal pz); void dBodyAddForceAtRelPos (dBodyID, dReal fx, dReal fy, dReal fz, dReal px, dReal py, dReal pz); void dBodyAddRelForceAtPos (dBodyID, dReal fx, dReal fy, dReal fz, dReal px, dReal py, dReal pz); void dBodyAddRelForceAtRelPos (dBodyID, dReal fx, dReal fy, dReal fz, dReal px, dReal py, dReal pz);
Add forces to bodies (absolute or relative coordinates). The forces are accumulated on to each body, and the accumulators are zeroed after each time step.
The ...RelForce and ...RelTorque functions take force vectors that are relative to the body's own frame of reference.
The ...ForceAtPos and ...ForceAtRelPos functions take an extra position vector (in global or body-relative coordinates respectively) that specifies the point at which the force is applied. All other functions apply the force at the center of mass.
const dReal * dBodyGetForce (dBodyID); const dReal * dBodyGetTorque (dBodyID);
Return the current accumulated force and torque vector. The returned pointers point to an array of 3 dReals. The returned values are pointers to internal data structures, so the vectors are only valid until any changes are made to the rigid body system.
void dBodySetForce (dBodyID b, dReal x, dReal y, dReal z); void dBodySetTorque (dBodyID b, dReal x, dReal y, dReal z);
Set the body force and torque accumulation vectors. This is mostly useful to zero the force and torque for deactivated bodies before they are reactivated, in the case where the force-adding functions were called on them while they were deactivated.
Kinematic State
void dBodySetDynamic (dBodyID); void dBodySetKinematic (dBodyID); int dBodyIsKinematic (dBodyID);
Bodies in the "kinematic" state (instead of the default, "dynamic" state) are "unstoppable" bodies, that behave as if they had infinite mass. This means they don't react to any force (gravity, constraints or user-supplied); they simply follow velocity to reach the next position. Their purpose is to animate objects that don't react to other bodies, but act upon them through joints (any joint, not just contact joints). For contact joints against moving geometry it's still faster to use the contact's motion parameters in a joint attached to the world ("null body"). Joints between two kinematic bodies, or against a kinematic body and the world, are completely ignored.
Note: setting the mass on a kinematic body will make it dynamic again. Calling dBodySetDynamic restores the original mass, so it's just a shortcut to dBodyGetMass followed by dBodySetMass.
Utility
void dBodyGetRelPointPos (dBodyID, dReal px, dReal py, dReal pz, dVector3 result); void dBodyGetRelPointVel (dBodyID, dReal px, dReal py, dReal pz, dVector3 result); void dBodyGetPointVel (dBodyID, dReal px, dReal py, dReal pz, dVector3 result);
Utility functions that take a point on a body (px,py,pz) and return that point's position or velocity in global coordinates (in result). The dBodyGetRelPointXXX functions are given the point in body relative coordinates, and the dBodyGetPointVel function is given the point in global coordinates.
void dBodyGetPosRelPoint (dBodyID, dReal px, dReal py, dReal pz, dVector3 result);
This is the inverse of dBodyGetRelPointPos. It takes a point in global coordinates (x,y,z) and returns the point's position in body-relative coordinates (result).
void dBodyVectorToWorld (dBodyID, dReal px, dReal py, dReal pz, dVector3 result); void dBodyVectorFromWorld (dBodyID, dReal px, dReal py, dReal pz, dVector3 result);
Given a vector expressed in the body (or world) coordinate system (x,y,z), rotate it to the world (or body) coordinate system (result).
Automatic Enabling and Disabling
Every body can be enabled or disabled. Enabled bodies participate in the simulation, while disabled bodies are turned off and do not get updated during a simulation step. New bodies are always created in the enabled state.
A disabled body that is connected through a joint to an enabled body will be automatically re-enabled at the next simulation step.
Disabled bodies do not consume CPU time, therefore to speed up the simulation bodies should be disabled when they come to rest. This can be done automatically with the auto-disable feature.
If a body has its auto-disable flag turned on, it will automatically disable itself when
- It has been idle for a given number of simulation steps.
- It has also been idle for a given amount of simulation time.
A body is considered to be idle when the magnitudes of both its linear velocity and angular velocity are below given thresholds.
Thus, every body has five auto-disable parameters: an enabled flag, a idle step count, an idle time, and linear/angular velocity thresholds. Newly created bodies get these parameters from world.
The following functions set and get the enable/disable parameters of a body.
void dBodyEnable (dBodyID); void dBodyDisable (dBodyID);
Manually enable and disable a body. Note that a disabled body that is connected through a joint to an enabled body will be automatically re-enabled at the next simulation step.
int dBodyIsEnabled (dBodyID);
Return 1 if a body is currently enabled or 0 if it is disabled.
void dBodySetAutoDisableFlag (dBodyID, int do_auto_disable); int dBodyGetAutoDisableFlag (dBodyID);
Set and get the auto-disable flag of a body. If the do_auto_disable is nonzero the body will be automatically disabled when it has been idle for long enough.
void dBodySetAutoDisableLinearThreshold (dBodyID, dReal linear_threshold); dReal dBodyGetAutoDisableLinearThreshold (dBodyID);
Set and get a body's linear velocity threshold for automatic disabling. The body's linear velocity magnitude must be less than this threshold for it to be considered idle. Set the threshold to dInfinity to prevent the linear velocity from being considered.
void dBodySetAutoDisableAngularThreshold (dBodyID, dReal angular_threshold); dReal dBodyGetAutoDisableAngularThreshold (dBodyID);
Set and get a body's angular velocity threshold for automatic disabling. The body's linear angular magnitude must be less than this threshold for it to be considered idle. Set the threshold to dInfinity to prevent the angular velocity from being considered.
void dBodySetAutoDisableSteps (dBodyID, int steps); int dBodyGetAutoDisableSteps (dBodyID);
Set and get the number of simulation steps that a body must be idle before it is automatically disabled. Set this to zero to disable consideration of the number of steps.
void dBodySetAutoDisableTime (dBodyID, dReal time); dReal dBodyGetAutoDisableTime (dBodyID);
Set and get the amount of simulation time that a body must be idle before it is automatically disabled. Set this to zero to disable consideration of the amount of simulation time.
void dBodySetAutoDisableAverageSamplesCount (dBodyID, unsigned int average_samples_count); int dBodyGetAutoDisableAverageSamplesCount (dBodyID);
To be written ...
void dBodySetAutoDisableDefaults (dBodyID);
Set the auto-disable parameters of the body to the default parameters that have been set on the world.
void dBodySetMovedCallback (dBodyID, void (*callback)(dBodyID));
Use it to register a function callback that is invoked whenever the body moves (that is, while it is not disabled). This is useful for integrating ODE with 3D engines, where 3D entities must be moved whenever a ODE body move. The callback must have the prototype void callback(dBodyID).
Damping
Damping serves two purposes: reduce simulation instability, and to allow the bodies to come to rest (and possibly auto-disabling them).
Bodies are constructed using the world's current damping parameters. Setting the scales to 0 disables the damping.
Here is how it is done: after every time step linear and angular velocities are tested against the corresponding thresholds. If they are above, they are multiplied by (1 - scale). So a negative scale value will actually increase the speed, and values greater than one will make the object oscillate every step; both can make the simulation unstable.
To disable damping just set the damping scale to zero.
Note: The velocities are damped after the stepper function has moved the object. Otherwise the damping could introduce errors in joints. First the joint constraints are processed by the stepper (moving the body), then the damping is applied.
Note: The damping happens right after the moved callback is called; this way it still possible use the exact velocities the body has acquired during the step. You can even use the callback to create your own customized damping.
dReal dBodyGetLinearDamping (dBodyID); dReal dBodyGetAngularDamping (dBodyID); void dBodySetLinearDamping (dBodyID, dReal scale); void dBodySetAngularDamping (dBodyID, dReal scale);
Set and get the body's damping scale. After setting a damping scale, the body will ignore the world's damping scale until dBodySetDampingDefaults() is called. If a scale was not set, it returns the world's damping scale.
void dBodySetDamping (dBodyID, dReal linear_scale, dReal angular_scale);
Convenience function to set both linear and angular scales at once.
dReal dBodyGetLinearDampingThreshold (dBodyID); dReal dBodyGetAngularDampingThreshold (dBodyID); void dBodySetLinearDampingThreshold (dBodyID, dReal threshold); void dBodySetAngularDampingThreshold (dBodyID, dReal threshold);
Set/Get the body's damping thresholds. The damping will be applied only if the linear/angular speed is above the threshold limit.
void dBodySetDampingDefaults (dBodyID);
Resets the damping settings to the current world's settings.
dReal dBodyGetMaxAngularSpeed (dBodyID); void dBodySetMaxAngularSpeed (dBodyID, dReal max_speed);
You can also limit the maximum angular speed. In contrast to the damping functions, the angular velocity is affected before the body is moved. This means that it will introduce errors in joints that are forcing the body to rotate too fast. Some bodies have naturally high angular velocities (like cars' wheels), so you may want to give them a very high (like the default, dInfinity) limit.
Miscellaneous Body Functions
void dBodySetData (dBodyID, void *data); void *dBodyGetData (dBodyID);
Get and set the body's user-data pointer.
void dBodySetFiniteRotationMode (dBodyID, int mode);
This function controls the way a body's orientation is updated at each time step. The mode argument can be:
- 0: An "infinitesimal" orientation update is used. This is fast to compute, but it can occasionally cause inaccuracies for bodies that are rotating at high speed, especially when those bodies are joined to other bodies. This is the default for every new body that is created.
- 1: A ``finite orientation update is used. This is more costly to compute, but will be more accurate for high speed rotations. Note however that high speed rotations can result in many types of error in a simulation, and this mode will only fix one of those sources of error.
int dBodyGetFiniteRotationMode (dBodyID);
Return the current finite rotation mode of a body (0 or 1).
void dBodySetFiniteRotationAxis (dBodyID, dReal x, dReal y, dReal z);
This sets the finite rotation axis for a body. This is axis only has meaning when the finite rotation mode is set (see dBodySetFiniteRotationMode).
If this axis is zero (0,0,0), full finite rotations are performed on the body.
If this axis is nonzero, the body is rotated by performing a partial finite rotation along the axis direction followed by an infinitesimal rotation along an orthogonal direction.
This can be useful to alleviate certain sources of error caused by quickly spinning bodies. For example, if a car wheel is rotating at high speed you can call this function with the wheel's hinge axis as the argument to try and improve its behavior.
void dBodyGetFiniteRotationAxis (dBodyID, dVector3 result);
Return the current finite rotation axis of a body.
int dBodyGetNumJoints (dBodyID);
Return the number of joints that are attached to this body.
dJointID dBodyGetJoint (dBodyID, int index);
Return a joint attached to this body, given by index. Valid indexes are 0 to n-1 where n is the value returned by dBodyGetNumJoints.
dWorldID dBodyGetWorld (dBodyID);
Retrieves the world attached to the given body.
void dBodySetGravityMode (dBodyID b, int mode); int dBodyGetGravityMode (dBodyID b);
Set/get whether the body is influenced by the world's gravity or not. If mode is nonzero it is, if mode is zero, it isn't. Newly created bodies are always influenced by the world's gravity.
dGeomID dBodyGetFirstGeom (dBodyID); dGeomID dBodyGetNextGeom (dGeomID);
Give access to all geoms associated with a body. Use dBodyGetFirstGeom() to retrieve the first geom, then call dBodyGetNextGeom() with the previous geom as argument, to retrieve the next.
Joint Types and Functions
Creating and Destroying Joints
dJointID dJointCreateBall (dWorldID, dJointGroupID); dJointID dJointCreateHinge (dWorldID, dJointGroupID); dJointID dJointCreateSlider (dWorldID, dJointGroupID); dJointID dJointCreateContact (dWorldID, dJointGroupID, const dContact *); dJointID dJointCreateUniversal (dWorldID, dJointGroupID); dJointID dJointCreateHinge2 (dWorldID, dJointGroupID); dJointID dJointCreatePR (dWorldID, dJointGroupID); dJointID dJointCreatePU (dWorldID, dJointGroupID); dJointID dJointCreatePiston (dWorldID, dJointGroupID); dJointID dJointCreateFixed (dWorldID, dJointGroupID); dJointID dJointCreateAMotor (dWorldID, dJointGroupID); dJointID dJointCreateLMotor (dWorldID, dJointGroupID); dJointID dJointCreatePlane2D (dWorldID, dJointGroupID); dJointID dJointCreateDBall (dWorldID, dJointGroupID); dJointID dJointCreateDHinge (dWorldID, dJointGroupID); dJointID dJointCreateTransmission (dWorldID, dJointGroupID);
Create a new joint of a given type. The joint is initially in "limbo" (i.e. it has no effect on the simulation) because it does not connect to any bodies. The joint group ID is 0 to allocate the joint normally. If it is nonzero the joint is allocated in the given joint group. The contact joint will be initialized with the given dContact structure.
void dJointDestroy (dJointID);
Destroy a joint, disconnecting it from its attached bodies and removing it from the world. However, if the joint is a member of a group then this function has no effect - to destroy that joint the group must be emptied or destroyed.
dJointGroupID dJointGroupCreate (int max_size);
Create a joint group. The max_size argument is now unused and should be set to 0. It is kept for backwards compatibility.
void dJointGroupDestroy (dJointGroupID);
Destroy a joint group. All joints in the joint group will be destroyed.
void dJointGroupEmpty (dJointGroupID);
Empty a joint group. All joints in the joint group will be destroyed, but the joint group itself will not be destroyed.
Miscellaneous Joint Functions
void dJointAttach (dJointID, dBodyID body1, dBodyID body2);
Attach the joint to some new bodies. If the joint is already attached, it will be detached from the old bodies first. To attach this joint to only one body, set body1 or body2 to zero - a zero body refers to the static environment. Setting both bodies to zero puts the joint into "limbo", i.e. it will have no effect on the simulation, but might require some setup work again when re-attaching.
Note : Some joints, like hinge-2 need to be attached to two bodies to work.
void dJointEnable (dJointID); void dJointDisable (dJointID); int dJointIsEnabled (dJointID);
Disabled joints are completely ignored during the simulation. Disabled joints don't lose the already computed information like anchors and axes.
void dJointSetData (dJointID, void *data); void *dJointGetData (dJointID);
Get and set the joint's user-data pointer.
int dJointGetType (dJointID);
Get the joint's type. One of the following constants will be returned:
| dJointTypeBall | A ball-and-socket joint. |
| dJointTypeHinge | A hinge joint. |
| dJointTypeSlider | A slider joint. |
| dJointTypeContact | A contact joint. |
| dJointTypeUniversal | A universal joint. |
| dJointTypeHinge2 | A hinge-2 joint. |
| dJointTypeFixed | A fixed joint. |
| dJointTypeAMotor | An angular motor joint. |
| dJointTypeLMotor | A linear motor joint. |
| dJointTypePlane2D | A Plane 2D joint. |
| dJointTypePR | A Prismatic-Rotoide joint. |
| dJointTypePU | A Prismatic-Universal joint. |
| dJointTypePiston | A Piston joint. |
| dJointTypeDBall | A Double Ball-And-Socket joint. |
| dJointTypeDHinge | A Double Hinge joint. |
| dJointTypeTransmission | A Transmission joint. |
dBodyID dJointGetBody (dJointID, int index);
Return the bodies that this joint connects. If index is 0 the "first" body will be returned, corresponding to the body1 argument of [#func_dJointAttach dJointAttach]. If index is 1 the "second" body will be returned, corresponding to the body2 argument of dJointAttach.
If one of these returned body IDs is zero, the joint connects the other body to the static environment. If both body IDs are zero, the joint is in "limbo" and has no effect on the simulation.
int dAreConnected (dBodyID, dBodyID);
Utility function: return 1 if the two bodies are connected together by a joint, otherwise return 0.
int dAreConnectedExcluding (dBodyID, dBodyID, int joint_type);
Utility function: return 1 if the two bodies are connected together by a joint that does not have type joint_type, otherwise return 0. joint_type is a dJointTypeXXX constant. This is useful for deciding whether to add contact joints between two bodies: if they are already connected by non-contact joints then it may not be appropriate to add contacts, however it is okay to add more contact between- bodies that already have contacts.
Joint feedback
void dJointSetFeedback (dJointID, dJointFeedback *); dJointFeedback *dJointGetFeedback (dJointID);
During the world time step, the forces that are applied by each joint are computed. These forces are added directly to the joined bodies, and the user normally has no way of telling which joint contributed how much force.
If this information is desired then the user must allocate a dJointFeedback structure and pass its pointer to the dJointSetFeedback() function. The feedback information structure is defined as follows:
typedef struct dJointFeedback {
dVector3 f1; // force that joint applies to body 1
dVector3 t1; // torque that joint applies to body 1
dVector3 f2; // force that joint applies to body 2
dVector3 t2; // torque that joint applies to body 2
} dJointFeedback;
During the time step any feedback structures that are attached to joints will be filled in with the joint's force and torque information. The dJointGetFeedback() function returns the current feedback structure pointer, or 0 if none is used (this is the default). dJointSetFeedback() can be passed 0 to disable feedback for that joint. Note that if the feedback structure was set, there is no need to use dJointGetFeedback(), since the structure was defined previously and you can check it after every simulation step. The getter is only useful if more than one piece of code wants to enable a feedback on a specific joint; in that case, you can check first if the joint already have a feedback, and not set another one - which would disable the first feedback set.
Are the returned values valid?
Issues about weird and inconsistent forces and torques in the feedback structure have been reported to the mailing list (e.g. July 2010, April 2009 February 2009, September 2008). Read this conversation too November 2012.
Apparently "as soon as you have a more or less complex system the feedbacks might produce inappropriate values. The constraints solver doesn't care if the forces are evenly distributed, as long as they produce the correct result (that is, they add up to the proper force when they are all applied to the respective bodies)" (ref).
API design notes
It might seem strange to require that users perform the allocation of these structures. Why not just store the data statically in each joint? The reason is that not all users will use the feedback information, and even when it is used not all joints will need it. It will waste memory to store it statically, especially as this structure could grow to store a lot of extra information in the future.
Why not have ODE allocate the structure itself, at the user's request? The reason is that contact joints (which are created and destroyed every time step) would require a lot of time to be spent in memory allocation if feedback is required. Letting the user do the allocation means that a better allocation strategy can be provided, e.g simply allocating them out of a fixed array.
The alternative to this API is to have a joint-force callback. This would work of course, but it has a few problems. First, callbacks tend to pollute APIs and sometimes require the user to go through unnatural contortions to get the data to the right place. Second, this would expose ODE to being changed in the middle of a step (which would have bad consequences), and there would have to be some kind of guard against this or a debugging check for it - which would complicate things.
Joint parameter setting functions
Ball and Socket
A ball and socket joint is shown in figure 4.
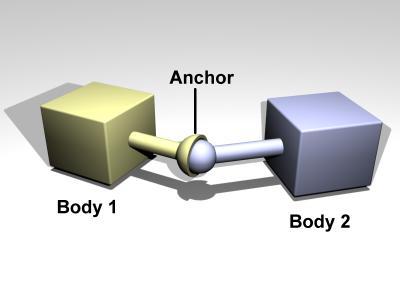
Figure 4: A ball and socket joint.
void dJointSetBallAnchor (dJointID, dReal x, dReal y, dReal z);
Set the joint anchor point. The joint will try to keep this point on each body together. The input is specified in world coordinates. If there is no body attached to the joint this function has not effect.
void dJointGetBallAnchor (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 1. If the joint is perfectly satisfied, this will be the same as the point on body 2.
void dJointGetBallAnchor2 (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 2. You can think of a ball and socket joint as trying to keep the result of dJointGetBallAnchor() and dJointGetBallAnchor2() the same. If the joint is perfectly satisfied, this function will return the same value as dJointGetBallAnchor to within roundoff errors. dJointGetBallAnchor2 can be used, along with dJointGetBallAnchor, to see how far the joint has come apart.
Hinge
A hinge joint is shown in figure 5.
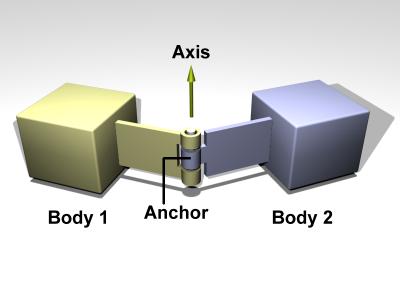
Figure 5: A hinge joint.
The default axis is:
- Axis 1: x=1, y=0, z=0
void dJointSetHingeAnchor (dJointID, dReal x, dReal y, dReal z);
Set hinge anchor parameters. The joint will try to keep this point on each body together. The input is specified in world coordinates. If there is no body attached to the joint this function has not effect.
void dJointSetHingeAxis (dJointID, dReal x, dReal y, dReal z);
Set hinge anchor and axis parameters. If there is no body attached to the joint this function has not effect.
void dJointGetHingeAnchor (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 1. If the joint is perfectly satisfied, this will be the same as the point on body 2.
void dJointGetHingeAnchor2 (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 2. If the joint is perfectly satisfied, this will return the same value as dJointGetHingeAnchor. If not, this value will be slightly different. This can be used, for example, to see how far the joint has come apart.
void dJointGetHingeAxis (dJointID, dVector3 result);
Get hinge axis parameter.
dReal dJointGetHingeAngle (dJointID); dReal dJointGetHingeAngleRate (dJointID);
Get the hinge angle and the time derivative of this value. The angle is measured between the two bodies, or between the body and the static environment. The angle will be between -pi..pi.
When the hinge anchor or axis is set, the current position of the attached bodies is examined and that position will be the zero angle.
Slider
A slider joint is shown in figure 6.
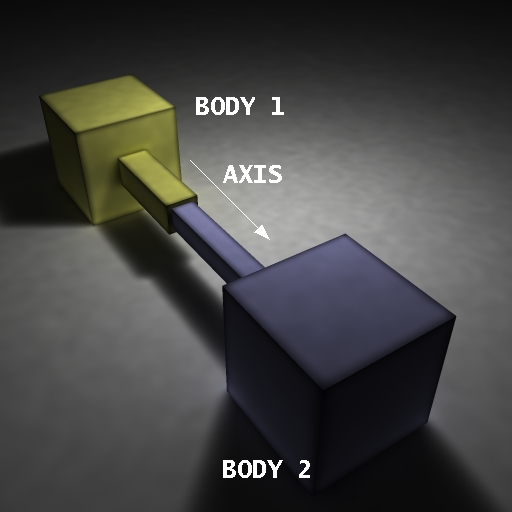
Figure 6: A slider joint.
The default axis is: Axis: x=1, y=0, z=0
void dJointSetSliderAxis (dJointID, dReal x, dReal y, dReal z);
Set the slider axis parameter.
void dJointGetSliderAxis (dJointID, dVector3 result);
Get the slider axis parameter.
dReal dJointGetSliderPosition (dJointID); dReal dJointGetSliderPositionRate (dJointID);
Get the slider linear position (i.e. the slider's "extension") and the time derivative of this value. If the axis is set such as pointing to Body 0 from Body 1 then the position and rate will be positive has the distance increase between the 2 bodies.
When the axis is set, the current position of the attached bodies is examined and that position will be the zero position.
Universal
A universal joint is shown in figure 7.
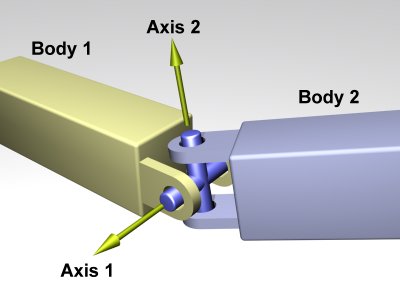
Figure 7: A universal joint.
A universal joint is like a ball and socket joint that constrains an extra degree of rotational freedom. Given axis 1 on body 1, and axis 2 on body 2 that is perpendicular to axis 1, it keeps them perpendicular. In other words, rotation of the two bodies about the direction perpendicular to the two axes will be equal.
In the picture, the two bodies are joined together by a cross. Axis 1 is attached to body 1, and axis 2 is attached to body 2. The cross keeps these axes at 90 degrees, so if you grab body 1 and twist it, body 2 will twist as well.
A Universal joint is equivalent to a hinge-2 joint where the hinge-2's axes are perpendicular to each other, and with a perfectly rigid connection in place of the suspension.
Universal joints show up in cars, where the engine causes a shaft, the drive shaft, to rotate along its own axis. At some point you'd like to change the direction of the shaft. The problem is, if you just bend the shaft, then the part after the bend won't rotate about its own axis. So if you cut it at the bend location and insert a universal joint, you can use the constraint to force the second shaft to rotate about the same angle as the first shaft.
Another use of this joint is to attach the arms of a simple virtual creature to its body. Imagine a person holding their arms straight out. You may want the arm to be able to move up and down, and forward and back, but not to rotate about its own axis.
The default axes are:
- Axis 1: x=1, y=0, z=0
- Axis 2: x=0, y=1, z=0
Note that as the two axes must be perpendicular, an attempt to set the first axis to the value of the second (or vice-versa) will result in an error at runtime even if the second axis is changed immediately afterwards.
Here are the universal joint functions:
void dJointSetUniversalAnchor (dJointID, dReal x, dReal y, dReal z);
Set the joint anchor point. The joint will try to keep this point on each body together. The input is specified in world coordinates. If there is no body attached to the joint this function has not effect.
void dJointSetUniversalAxis1 (dJointID, dReal x, dReal y, dReal z); void dJointSetUniversalAxis2 (dJointID, dReal x, dReal y, dReal z);
Set universal anchor and axis parameters. Axis 1 and axis 2 should be perpendicular to each other.
void dJointGetUniversalAnchor (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 1. If the joint is perfectly satisfied, this will be the same as the point on body 2.
void dJointGetUniversalAnchor2 (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 2. You can think of the ball and socket part of a universal joint as trying to keep the result of dJointGetBallAnchor() and dJointGetBallAnchor2() the same. If the joint is perfectly satisfied, this function will return the same value as dJointGetUniversalAnchor to within roundoff errors. dJointGetUniversalAnchor2 can be used, along with dJointGetUniversalAnchor, to see how far the joint has come apart.
void dJointGetUniversalAxis1 (dJointID, dVector3 result); void dJointGetUniversalAxis2 (dJointID, dVector3 result);
Get universal axis parameters.
dReal dJointGetUniversalAngle1 (dJointID); dReal dJointGetUniversalAngle2 (dJointID); dReal dJointGetUniversalAngles (dJointID, dReal *angle1, dReal *angle2); dReal dJointGetUniversalAngle1Rate (dJointID); dReal dJointGetUniversalAngle2Rate (dJointID);
Get the universal angles and the time derivatives of these values. The angle is measured between a body and the cross, or between the static environment and the cross. The angle will be between -pi..pi.
When the universal anchor or axis is set, the current position of the attached bodies is examined and that position will be the zero angle.
Hinge-2
A hinge-2 joint is shown in figure 8.
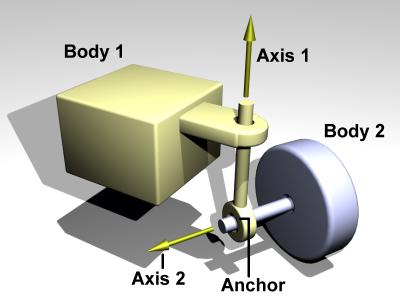
Figure 8: A hinge-2 joint.
The hinge-2 joint is the same as two hinges connected in series, with different hinge axes. An example, shown in the above picture is the steering wheel of a car, where one axis allows the wheel to be steered and the other axis allows the wheel to rotate.
The hinge-2 joint has an anchor point and two hinge axes. Axis 1 is specified relative to body 1 (this would be the steering axis if body 1 is the chassis). Axis 2 is specified relative to body 2 (this would be the wheel axis if body 2 is the wheel).
Axis 1 can have joint limits and a motor, axis 2 can only have a motor.
Axis 1 can function as a suspension axis, i.e. the constraint can be compressible along that axis.
The hinge-2 joint where axis1 is perpendicular to axis 2 is equivalent to a universal joint with added suspension.
Default axes are:
- Axis 1: x=1, y=0, z=0
- Axis 2: x=0, y=1, z=0
void dJointSetHinge2Anchor (dJointID, dReal x, dReal y, dReal z);
Set hinge-2 anchor parameters. The joint will try to keep this point on each body together. The input is specified in world coordinates. If there is no body attached to the joint this function has not effect.
void dJointSetHinge2Axis1 (dJointID, dReal x, dReal y, dReal z); void dJointSetHinge2Axis2 (dJointID, dReal x, dReal y, dReal z);
Set axis parameters. Axis 1 and axis 2 must not lie along the same line.
void dJointGetHinge2Anchor (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 1. If the joint is perfectly satisfied, this will be the same as the point on body 2.
void dJointGetHinge2Anchor2 (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 2. If the joint is perfectly satisfied, this will return the same value as dJointGetHinge2Anchor. If not, this value will be slightly different. This can be used, for example, to see how far the joint has come apart.
void dJointGetHinge2Axis1 (dJointID, dVector3 result); void dJointGetHinge2Axis2 (dJointID, dVector3 result);
Get hinge-2 axis parameters.
dReal dJointGetHinge2Angle1 (dJointID); dReal dJointGetHinge2Angle1Rate (dJointID); dReal dJointGetHinge2Angle2Rate (dJointID);
Note: There is currently no function call for getting the value of the second angle.
Get the hinge-2 angles (around axis 1 and axis 2) and the time derivatives of these values.
When the anchor or axis is set, the current position of the attached bodies is examined and that position will be the zero angle.
Prismatic and Rotoide
A PR joint is shown in figure 9.
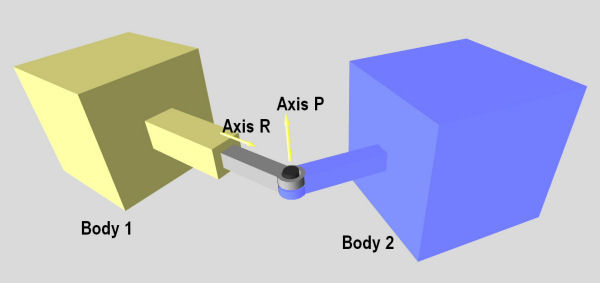
Figure 9: A PR joint.
A prismatic and rotoide joint (JointPR) combines a Slider (prismatic) and a Hinge (rotoide). It can be used to decrease the number of bodies in a simulation. Usually you cannot attach 2 ODE joints together they need a body in between. An example of use of this type of joint can be in the creation of a hydraulic piston.
You can set the position of the body2 with respect to the rotoide articulation by setting the anchor point of this joint. (As for the Hinge joint).
An offset is calculated when the joint is created and this offset is the distance between the body1 and the rotoide articulation. Retrieving the position of the joint will give you the position with respect to this offset.
The first axis is the prismatic axis. Its parameters accessed with the [#limit_motor_parameter dParamX] flag.
The second axis is the rotoide axis. Its parameters can be accessed with the [#limit_motor_parameter dParamX2] flag.
Default axes are:
- Axis R: x=1, y=0, z=0.
- Axis P: x=0, y=1, z=0
void dJointSetPRAxis1 (dJointID, dReal x, dReal y, dReal z); void dJointGetPRAxis1 (dJointID, dVector3 result);
Set/Get the axis for the prismatic articulation.
void dJointSetPRAxis2 (dJointID, dReal x, dReal y, dReal z); void dJointGetPRAxis2 (dJointID, dVector3 result);
Set/Get the axis for the rotoide articulation.
void dJointSetPRAnchor (dJointID, dReal x, dReal y, dReal z); void dJointGetPRAnchor (dJointID, dVector3 result);
Set PR anchor parameter. The joint will try to keep distance between body2 and the rotoide acticulation fixed. The input is specified in world coordinates. If there is no body2 attached to the joint this function has not effect.
dReal dJointGetPRPosition (dJointID);
Get the PR linear position (i.e. the prismatic's extension)
When the axis is set, the current position of body1 and the anchor is examined and that position will be the zero position.
The position is the "oriented" length between the body1 and and the rotoide articulation. position = (Prismatic axis) dot_product [(body1 + offset) - (body2 + anchor2)]
Important: The 2 axis must not be parallel. Since this is a new joint only when the 2 joint are at 90deg of each other was fully tested.
Prismatic - Universal
A Prismatic - Universal joint is shown in figure 10.
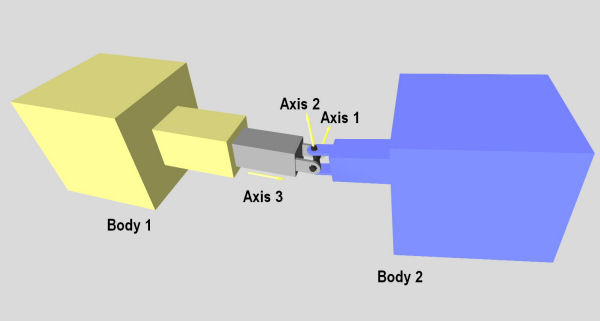
Figure 10: A Prismatic - Universal joint.
A prismatic-Universal joint (JointPU) combines a Slider (prismatic) between body1 and the anchor and a Universal joint at the anchor position. This joint provide 1 degree of freedom in translation and 2 degrees of freedom in rotation.
It was possible to achieve the same result by combining a Slider and a Universal joint but a dummy body was needed between the 2 joints. This joint can be used to decrease the number of bodies in a simulation.
The first axis is the first universal axis. Its parameters accessed with the dParamX1 or dParamX flag (Ex: dParamFMax1).
The second axis is the second universal axis. Its parameters can be accessed with the dParamX2 flag (Ex: dParamFMax2).
The third axis is the prismatic axis. Its parameters can be accessed with the dParamX3 flag (Ex: dParamFMax3).
Default axes are:
- Axis 1: x=0, y=1, z=0.
- Axis 2: x=0, y=0, z=1.
- Axis 3: x=1, y=0, z=0.
dReal dJointGetPUPosition (dJointID);
Get the PU linear position (i.e. the prismatic's extension)
When the anchor is set, the current position of body1 and the anchor is examined and that position will be the zero position (initial_offset) (i.e. dJointGetPUPosition with the body1 at that position with respect to the anchor will return 0.0).
The position is the "oriented" length between the body1 and and the universal articulation (anchor). position = { (Prismatic axis) dot_product [body1 - anchor] } - initial_offset
dReal dJointGetPUPositionRate (dJointID);
Get time derivative of the position.
void dJointSetPUAnchor (dJointID, dReal x, dReal y, dReal z); void dJointGetPUAnchor (dJointID, dVector3 result);
Set the PU anchor parameter. The joint will try to keep distance between body2 and the universal articulation fixed. The input is specified in world coordinates. If there is no body2 attached to the joint this function has not effect.
void dJointSetPUAnchorDelta (dJointID, dReal x, dReal y, dReal z, dReal dx, dReal dy, dReal dz);
Set the PU anchor and the relative position of each body as if body1 was at its current position + [dx,dy,dy] (dx, dy, dx in world frame).
This is like setting the joint with the prismatic part already elongated or compressed.
After setting the anchor with a delta if the function dJointGetPUPosition is called the answer will be: sqrt(dx*dx + dy*dy + dz*dz) * Normalize[axis3 dot_product (dx,dy,dz)]
void dJointSetPUAxis1 (dJointID, dReal x, dReal y, dReal z); void dJointGetPUAxis1 (dJointID, dVector3 result); void dJointSetPUAxis2 (dJointID, dReal x, dReal y, dReal z); void dJointGetPUAxis2 (dJointID, dVector3 result);
Set/Get universal axis parameters. Axis 1 and axis 2 should be perpendicular to each other.
void dJointSetPUAxis3 (dJointID, dReal x, dReal y, dReal z); void dJointGetPUAxis3 (dJointID, dVector3 result);
Set/Get the axis for the prismatic articulation.
void dJointSetPUAxisP (dJointID, dReal x, dReal y, dReal z); void dJointGetPUAxisP (dJointID, dVector3 result);
This is another name for function dJointSetPUAxis3
void dJointGetPUAngles (dJointID, dReal *angle1, dReal *angle2); dReal dJointGetPUAngle1 (dJointID); dReal dJointGetPUAngle2 (dJointID); dReal dJointGetPUAngle1Rate (dJointID); dReal dJointGetPUAngle2Rate (dJointID);
Get the universal angles and the time derivatives of these values. The angle is measured between a body and the cross, or between the static environment and the cross. The angle will be between -pi..pi.
When the universal anchor or axis is set, the current position of the attached bodies is examined and that position will be the zero angle.
Piston
Piston joint is shown in figure 11.
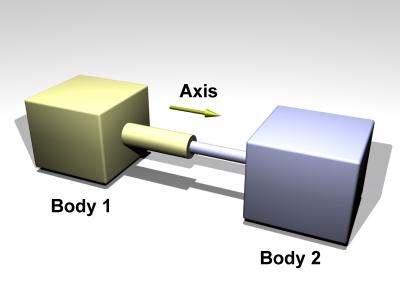
Figure 11: A Piston joint.
A piston joint is similar to a Slider joint except that rotation around the translation axis is possible.
The default axis is: Axis: x=1, y=0, z=0
void dJointSetPistonAnchor (dJointID, dReal x, dReal y, dReal z); void dJointGetPistonAnchor (dJointID, dVector3 result);
Set piston anchor parameters. The joint will try to keep the distance of this point fixed with respect to body2. The input is specified in world coordinates. If there is no body attached to the joint this function has not effect.
void dJointGetPistonAnchor2 (dJointID, dVector3 result);
Get the joint anchor point, in world coordinates. This returns the point on body 2. If the joint is perfectly satisfied, this will return the same value as dJointGetPistonAnchor. If not, this value will be slightly different. This can be used, for example, to see how far the joint has come apart.
void dJointSetPistonAxis (dJointID, dReal x, dReal y, dReal z); void dJointGetPistonAxis (dJointID, dVector3 result);
Set/Get piston axis parameters.
When the piston axis is set, the current position of the attached bodies is examined and that position will be the zero angle.
void dJointSetPistonAxisDelta (dJointID j, dReal x, dReal y, dReal z, dReal dx, dReal dy, dReal dz); dReal dJointGetPistonPosition (dJointID); dReal dJointGetPistonPositionRate (dJointID);
Get the Piston linear position (i.e. the prismatic's extension)
When the anchor is set, the current position of body1 and the anchor is examined and that position will be the zero position (initial_offset) (i.e. dJointGetPUPosition with the body1 at that position with respect to the anchor will return 0.0).
The position is the "oriented" length between the body1 and and the anchor. position = { (Prismatic axis) dot_product [body1 - anchor] } - initial_offset
dReal dJointGetPistonAngle (dJointID); dReal dJointGetPistonAngleRate (dJointID);
Get the angle and the time derivative of this value. The angle is measured between the two bodies, or between the body and the static environment. The angle will be between -pi..pi. The only possible axis of rotation is the one defined by the dJointSetPistonAxis.
When the piston anchor or axis is set, the current position of the attached bodies is examined and that position will be the zero angle.
void dJointAddPistonForce (dJointID j, dReal force)
This function create a force inside the piston and this force will be applied on the 2 bodies.
Then force is apply to the center of mass of each body and the orientation of the force vector is along the axis of the piston.
Fixed
The fixed joint maintains a fixed relative position and orientation between two bodies, or between a body and the static environment. Using this joint is almost never a good idea in practice, except when debugging. If you need two bodies to be glued together it is better to represent that as a single body.
void dJointSetFixed (dJointID);
Call this on the fixed joint after it has been attached to remember the current desired relative offset and desired relative rotation between the bodies.
Contact
A contact joint is shown in figure 10.
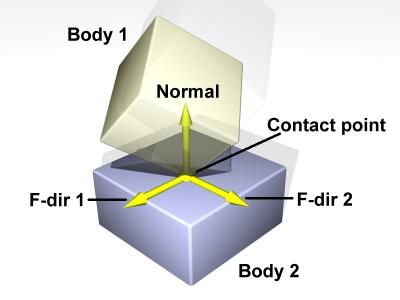
Figure 10: A contact joint.
The contact joint prevents body 1 and body 2 from inter-penetrating at the contact point. It does this by only allowing the bodies to have an "outgoing" velocity in the direction of the contact normal. Contact joints typically have a lifetime of one time step. They are created and deleted in response to collision detection.
Contact joints can simulate friction at the contact by applying special forces in the two friction directions that are perpendicular to the normal.
When a contact joint is created, a dContact structure must be supplied. This has the following definition:
struct dContact {
dSurfaceParameters surface;
dContactGeom geom;
dVector3 fdir1;
};
geom is a substructure that is set by the collision functions. It is described in the collision section.
fdir1 is a "first friction direction" vector that defines a direction along which frictional force is applied. It must be of unit length and perpendicular to the contact normal (so it is typically tangential to the contact surface). It should only be defined if the dContactFDir1 flag is set in surface.mode. The "second friction direction" is a vector computed to be perpendicular to both the contact normal and fdir1.
surface is a substructure that is set by the user. Its members define the properties of the colliding surfaces. It has the following definition:
struct dSurfaceParameters {
int mode;
dReal mu;
dReal mu2;
dReal rho;
dReal rho2;
dReal rhoN;
dReal bounce;
dReal bounce_vel;
dReal soft_erp;
dReal soft_cfm;
dReal motion1, motion2, motionN;
dReal slip1, slip2;
};
- mode - Contact flags. This must always be set. This is a combination of one or more of the following flags:
| dContactMu2 | If not set, use mu for both friction directions. If set, use mu for friction direction 1, use mu2 for friction direction 2. |
| dContactFDir1 | If set, take fdir1 as friction direction 1, otherwise automatically compute friction direction 1 to be perpendicular to the contact normal (in which case its resulting orientation is unpredictable). |
| dContactBounce | If set, the contact surface is bouncy, in other words the bodies will bounce off each other. The exact amount of bouncyness is controlled by the bounce parameter. |
| dContactSoftERP | If set, the error reduction parameter of the contact normal can be set with the soft_erp parameter. This is useful to make surfaces soft.
|
| dContactSoftCFM | If set, the constraint force mixing parameter of the contact normal can be set with the soft_cfm parameter. This is useful to make surfaces soft.
|
| dContactMotion1 | If set, the contact surface is assumed to be moving independently of the motion of the bodies. This is kind of like a conveyor belt running over the surface. When this flag is set, motion1 defines the surface velocity in friction direction 1. |
| dContactMotion2 | The same thing as above, but for friction direction 2. |
| dContactMotionN | The same thing as above, but along the contact normal. |
| dContactSlip1 | Force-dependent-slip (FDS) in friction direction 1. |
| dContactSlip2 | Force-dependent-slip (FDS) in friction direction 2. |
| dContactRolling | Enables rolling/spinning friction. |
| dContactApprox1_1 | Use the friction pyramid approximation for friction direction 1. If this is not specified then the constant-force-limit approximation is used (and mu is a force limit). |
| dContactApprox1_2 | Use the friction pyramid approximation for friction direction 2. If this is not specified then the constant-force-limit approximation is used (and mu is a force limit). |
| dContactApprox1_N | Use the friction pyramid approximation for spinning (rolling around normal). |
| dContactApprox1 | Equivalent to dContactApprox1_1, dContactApprox1_2 and dContactApprox1_N.
|
- mu : Coulomb friction coefficient. This must be in the range 0 to
dInfinity. 0 results in a frictionless contact, anddInfinityresults in a contact that never slips. Note that frictionless contacts are less time consuming to compute than ones with friction, and infinite friction contacts can be cheaper than contacts with finite friction. This must always be set.
- mu2 : Optional Coulomb friction coefficient for friction direction 2 (0..
dInfinity). This is only used if the corresponding flag is set inmode.
- rho: Rolling friction coefficient around direction 1.
- rho2: Rolling friction coefficient around direction 2.
- rhoN: Rolling friction coefficient around the normal direction.
- bounce : Restitution parameter (0..1). 0 means the surfaces are not bouncy at all, 1 is maximum bouncyness. This is only used if the corresponding flag is set in
mode.
- bounce_vel : The minimum incoming velocity necessary for bounce. Incoming velocities below this will effectively have a bounce parameter of 0. This is only used if the corresponding flag is set in
mode.
- soft_erp : Contact normal "softness" parameter. This is only used if the corresponding flag is set in
mode.
- soft_cfm : Contact normal "softness" parameter. This is only used if the corresponding flag is set in
mode.
- motion1, motion2, motionN : Surface velocity in friction directions 1 and 2 and along the normal. These are only used if the corresponding flags are set in
mode.
- slip1, slip2 : The coefficients of force-dependent-slip (FDS) for friction directions 1 and 2. These are only used if the corresponding flags are set in
mode.
FDS is an effect that causes the contacting surfaces to side past each other with a velocity that is proportional to the force that is being applied tangentially to that surface.
Consider a contact point where the coefficient of friction mu is infinite. Normally, if a force [math]\displaystyle{ \textbf{f} }[/math] is applied to the two contacting surfaces, to try and get them to slide past each other, they will not move. However, if the FDS coefficient is set to a positive value [math]\displaystyle{ k }[/math] then the surfaces will slide past each other, building up to a steady velocity of [math]\displaystyle{ k \textbf{f} }[/math] relative to each other.
Note that this is quite different from normal frictional effects: the force does not cause a constant acceleration of the surfaces relative to each other - it causes a brief acceleration to achieve the steady velocity.
This is useful for modeling some situations, in particular tires. For example consider a car at rest on a road. Pushing the car in its direction of travel will cause it to start moving (i.e. the tires will start rolling). Pushing the car in the perpendicular direction will have no effect, as the tires do not roll in that direction. However - if the car is moving at with speed [math]\displaystyle{ v }[/math], applying a force [math]\displaystyle{ \textbf{f} }[/math] in the perpendicular direction will cause the tires to slip on the road with a velocity proportional to [math]\displaystyle{ v \textbf{f} }[/math] (Yes, this really happens).
To model this in ODE set the tire-road contact parameters as follows: set friction direction 1 in the direction that the tire is rolling in, and set the FDS slip coefficient in friction direction 2 to [math]\displaystyle{ k v }[/math], where [math]\displaystyle{ v }[/math] is the tire rolling velocity and [math]\displaystyle{ k }[/math] is a tire parameter that you can chose based on experimentation.
Note that FDS is quite separate from the sticking/slipping effects of Coulomb friction - both modes can be used together at a single contact point.
Angular Motor
An angular motor (AMotor) allows the relative angular velocities of two bodies to be controlled. The angular velocity can be controlled on up to three axes, allowing torque motors and stops to be set for rotation about those axes (see the "[#Stops_and_motor_parameters Stops and motor parameters]" section below). This is mainly useful in conjunction will ball joints (which do not constrain the angular degrees of freedom at all), but it can be used in any situation where angular control is needed. To use an AMotor with a ball joint, simply attach it to the same two bodies that the ball joint is attached to.
The AMotor can be used in different modes. In dAMotorUser mode, the user directly sets the axes that the AMotor controls. In dAMotorEuler mode, AMotor computes the euler angles corresponding to the relative rotation, allowing euler angle torque motors and stops to be set. An AMotor joint with euler angles is shown in figure 11.
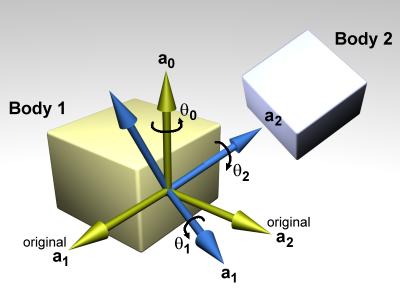
Figure 11: An AMotor joint with euler angles.
In this diagram, a0, a1 and a2 are the three axes along which angular motion is controlled. The green axes (including a0) are anchored to body 1. The blue axes (including a2) are anchored to body 2. To get the body 2 axes from the body 1 axes the following sequence of rotations is performed:
- Rotate by theta 0 about a0.
- Rotate by theta 1 about a1 (a1 has been rotated from its original position).
- Rotate by theta 2 about a2 (a2 has been rotated twice from its original position).
There is an important restriction when using euler angles: the theta 1 angle must not be allowed to get outside the range - pi /2 ... pi /2. If this happens then the AMotor joint will become unstable (there is a singularity at +/- pi /2). Thus you must set the appropriate stops on axis number 1.
void dJointSetAMotorMode (dJointID, int mode); int dJointGetAMotorMode (dJointID);
Set (and get) the angular motor mode. The mode parameter must be one of the following constants:
| dAMotorUser | The AMotor axes and joint angle settings are entirely controlled by the user. This is the default mode. |
| dAMotorEuler | Euler angles are automatically computed. The axis a1 is also automatically computed. The AMotor axes must be set correctly when in this mode, as described below. When this mode is initially set the current relative orientations of the bodies will correspond to all euler angles at zero. |
void dJointSetAMotorNumAxes (dJointID, int num); int dJointGetAMotorNumAxes (dJointID);
Set (and get) the number of angular axes that will be controlled by the AMotor. The argument num can range from 0 (which effectively deactivates the joint) to 3. This is automatically set to 3 in dAMotorEuler mode.
void dJointSetAMotorAxis (dJointID, int anum, int rel, dReal x, dReal y, dReal z); void dJointGetAMotorAxis (dJointID, int anum, dVector3 result); int dJointGetAMotorAxisRel (dJointID, int anum);
Set (and get) the AMotor axes. The anum argument selects the axis to change (0,1 or 2). Each axis can have one of three "relative orientation" modes, selected by rel:
- 0: The axis is anchored to the global frame.
- 1: The axis is anchored to the first body.
- 2: The axis is anchored to the second body.
The axis vector (x,y,z) is always specified in global coordinates regardless of the setting of rel. There are two GetAMotorAxis functions, one to return the axis and one to return the relative mode.
For dAMotorEuler mode:
- Only axes 0 and 2 need to be set. Axis 1 will be determined automatically at each time step.
- Axes 0 and 2 must be perpendicular to each other.
- Axis 0 must be anchored to the first body, axis 2 must be anchored to the second body.
void dJointSetAMotorAngle (dJointID, int anum, dReal angle);
Tell the AMotor what the current angle is along axis anum. This function should only be called in dAMotorUser mode, because in this mode the AMotor has no other way of knowing the joint angles. The angle information is needed if stops have been set along the axis, but it is not needed for axis motors.
dReal dJointGetAMotorAngle (dJointID, int anum);
Return the current angle for axis anum. In dAMotorUser mode this is simply the value that was set with dJointSetAMotorAngle. In dAMotorEuler mode this is the corresponding euler angle.
dReal dJointGetAMotorAngleRate (dJointID, int anum);
Return the current angle rate for axis anum. In dAMotorUser mode this is always zero, as not enough information is available. In dAMotorEuler mode this is the corresponding euler angle rate.
Linear Motor
A linear motor (LMotor) allows the relative linear velocities of two bodies to be controlled. The linear velocity can be controlled on up to three axes, allowing torque motors and stops to be set for translation along those axes (see the "[#Stops_and_motor_parameters Stops and motor parameters]" section below).
void dJointSetLMotorNumAxes (dJointID, int num); int dJointGetLMotorNumAxes (dJointID);
Set (and get) the number of axes that will be controlled by the LMotor. The argument num can range from 0 (which effectively deactivates the joint) to 3.
void dJointSetLMotorAxis (dJointID, int anum, int rel, dReal x, dReal y, dReal z); void dJointGetLMotorAxis (dJointID, int anum, dVector3 result);
Set (and get) the LMotor axes. The anum argument selects the axis to change (0,1 or 2). Each axis can have one of three "relative orientation" modes, selected by rel:
- 0: The axis is anchored to the global frame.
- 1: The axis is anchored to the first body.
- 2: The axis is anchored to the second body.
The axis vector (x,y,z) is always specified in global coordinates regardless of the setting of rel.
Plane 2D
The plane-2d joint acts on a body and constrains it to the Z == 0 plane. Some drift may still occur due to numerical inaccuracies, so bodies must be reset after each frame using some code like this:
const dReal *rot = dBodyGetAngularVel (my_body.id()));
const dReal *quat_ptr;
dReal quat[4],
quat_len;
quat_ptr = dBodyGetQuaternion (my_body.id()));
quat[0] = quat_ptr[0];
quat[1] = 0;
quat[2] = 0;
quat[3] = quat_ptr[3];
quat_len = sqrt (quat[0] * quat[0] + quat[3] * quat[3]);
quat[0] /= quat_len;
quat[3] /= quat_len;
dBodySetQuaternion (my_body.id()), quat);
dBodySetAngularVel (my_body.id()), 0, 0, rot[2]);
Double Ball And Socket
The double ball joint (also known as a "distance joint") keeps two anchor points (one from each body) at a fixed distance apart. This distance is deduced by the relative positions of the anchor points during dJointAttach(), or can be set manually later.
TODO: add picture
void dJointSetDBallAnchor1(dJointID, dReal x, dReal y, dReal z); void dJointSetDBallAnchor2(dJointID, dReal x, dReal y, dReal z); void dJointGetDBallAnchor1(dJointID, dVector3 result); void dJointGetDBallAnchor2(dJointID, dVector3 result);
Sets and gets the anchors. Anchor 1 is attached to body 1, anchor 2 is attached to body 2.
dReal dJointGetDBallDistance(dJointID);
Returns the target distance between the anchors. The actual distance between the anchors may differ due to joint errors.
void dJointSetDBallDistance(dJointID, dReal dist);
Manually sets the target distance the joint will try to maintain. This overrides the value automatically computed during dJointAttach().
Double Hinge
The Double Hinge joint is like the Hinge2 joint, but both axes are the same.
TODO: add picture
void dJointSetDHingeAxis(dJointID, dReal x, dReal y, dReal z); void dJointGetDHingeAxis(dJointID, dVector3 result);
Sets and gets the axis for both hinges.
void dJointSetDHingeAnchor1(dJointID, dReal x, dReal y, dReal z); void dJointSetDHingeAnchor2(dJointID, dReal x, dReal y, dReal z); void dJointGetDHingeAnchor1(dJointID, dVector3 result); void dJointGetDHingeAnchor2(dJointID, dVector3 result);
Sets and gets the anchors. Anchor 1 is attached to body 1, anchor 2 is attached to body 2.
dReal dJointGetDHingeDistance(dJointID);
Returns the distance between the anchors.
Transmission
The transmission joint transmits torque from one body to another. It works in 3 modes:
- Intersecting-axes: simulates intersecting-axes beveled gears
- Parallel-axes: simulates parallel-axes gears
- Chain-drive: simulate chain and sprockets
TODO: a picture is needed here
void dJointSetTransmissionMode( dJointID j, int mode ); int dJointGetTransmissionMode( dJointID j );
Set and get the mode of the transmission joint. mode can be one of:
- dTransmissionIntersectingAxes
- dTransmissionParallelAxes
- dTransmissionChainDrive
void dJointGetTransmissionContactPoint1(dJointID, dVector3 result); void dJointGetTransmissionContactPoint2(dJointID, dVector3 result);
Gets the contact points for the first and second wheel.
void dJointSetTransmissionAxis1(dJointID, dReal x, dReal y, dReal z); void dJointSetTransmissionAxis2(dJointID, dReal x, dReal y, dReal z); void dJointGetTransmissionAxis1(dJointID, dVector3 result); void dJointGetTransmissionAxis2(dJointID, dVector3 result);
Intersecting-axes mode: Sets and gets the axes for the first and second bodies.
void dJointSetTransmissionAnchor1(dJointID, dReal x, dReal y, dReal z); void dJointSetTransmissionAnchor2(dJointID, dReal x, dReal y, dReal z); void dJointGetTransmissionAnchor1(dJointID, dVector3 result); void dJointGetTransmissionAnchor2(dJointID, dVector3 result);
Set and get the anchor points for each body.
void dJointSetTransmissionRatio( dJointID j, dReal ratio );
Parallel-axes mode only: Set the angular speed ratio between the gears. For the other modes the ratio is derived from the intersection angle or wheel radii.
dReal dJointGetTransmissionRatio( dJointID j );
Get the angular speed ratio between the gears.
void dJointSetTransmissionAxis( dJointID j, dReal x, dReal y, dReal z ); void dJointGetTransmissionAxis( dJointID j, dVector3 result );
Parallel-axes and chain-drive mode only. Set and get the axes used for both wheels.
dReal dJointGetTransmissionAngle1( dJointID j ); dReal dJointGetTransmissionAngle2( dJointID j );
Get the phase, that is the traversed angle for the first and second wheel.
dReal dJointGetTransmissionRadius1( dJointID j ); dReal dJointGetTransmissionRadius2( dJointID j );
Get the radius of each wheel of the joint.
void dJointSetTransmissionRadius1( dJointID j, dReal radius ); void dJointSetTransmissionRadius2( dJointID j, dReal radius );
Chain-drive mode only: set the radius of each wheel. The radii is implicit in the other modes.
void dJointSetTransmissionBacklash( dJointID j, dReal backlash ); dReal dJointGetTransmissionBacklash( dJointID j );
Set and get the backlash of the joint.
Backlash is the clearance in the mesh of the wheels of the transmission, and is defined as the maximum distance that the geometric contact point can travel without any actual contact or transfer of power between the wheels. This can be converted in radians of revolution for each wheel by dividing by the wheel's radius.
To further illustrate this consider the situation where a wheel of radius [math]\displaystyle{ r_1 }[/math] is driving another wheel of radius [math]\displaystyle{ r_2 }[/math] and there is an amount of backlash equal to [math]\displaystyle{ b }[/math] in their mesh. If the driving wheel were to instantaneously stop there would be no contact, and hence the driven wheel would continue to turn for another [math]\displaystyle{ b / r_2 }[/math] radians until all the backlash in the mesh was taken up and contact restored. The backlash is therefore given in untis of length.
General
The joint geometry parameter setting functions should only be called after the joint has been attached to bodies, and those bodies have been correctly positioned, otherwise the joint may not be initialized correctly. If the joint is not already attached, these functions will do nothing.
For the parameter getting functions, if the system is out of alignment (i.e. there is some joint error) then the anchor/axis values will be correct with respect to body 1 only (or body 2 if you specified body 1 as zero in the dJointAttach function).
The default anchor for all joints is (0,0,0). The default axis for all joints is (1,0,0).
When an axis is set it will be normalized to unit length. The adjusted axis is what the axis getting functions will return.
When measuring a joint angle or position, a value of zero corresponds to the initial position of the bodies relative to each other.
Note that there are no functions to set joint angles or positions (or their rates) directly, instead you must set the corresponding body positions and velocities.
Stops and motor parameters
When a joint is first created there is nothing to prevent it from moving through its entire range of motion. For example a hinge will be able to move through its entire angle, and a slider will slide to any length.
This range of motion can be limited by setting stops on the joint. The joint angle (or position) will be prevented from going below the low stop value, or from going above the high stop value. Note that a joint angle (or position) of zero corresponds to the initial body positions.
As well as stops, many joint types can have motors. A motor applies a torque (or force) to a joint's degree(s) of freedom to get it to pivot (or slide) at a desired speed. Motors have force limits, which means they can apply no more than a given maximum force/torque to the joint.
Motors have two parameters: a desired speed, and the maximum force that is available to reach that speed. This is a very simple model of real life motors, engines or servos. However, is it quite useful when modeling a motor (or engine or servo) that is geared down with a gearbox before being connected to the joint. Such devices are often controlled by setting a desired speed, and can only generate a maximum amount of power to achieve that speed (which corresponds to a certain amount of force available at the joint).
Motors can also be used to accurately model dry (or Coulomb) friction in joints. Simply set the desired velocity to zero and set the maximum force to some constant value - then all joint motion will be impeded by that force.
The alternative to using joint stops and motors is to simply apply forces to the affected bodies yourself. Applying motor forces is easy, and joint stops can be emulated with restraining spring forces. However applying forces directly is often not a good approach and can lead to severe stability problems if it is not done carefully.
Consider the case of applying a force to a body to achieve a desired velocity. To calculate this force [math]\displaystyle{ F }[/math] you use information about the current velocity, something like this:
- [math]\displaystyle{ F = k (\text{desired speed} - \text{current speed}) }[/math]
This has several problems. First, the parameter [math]\displaystyle{ k }[/math] must be tuned by hand. If it is too low the body will take a long time to come up to speed. If it is too high the simulation will become unstable. Second, even if [math]\displaystyle{ k }[/math] is chosen well the body will still take a few time steps to come up to speed. Third, if any other "external" forces are being applied to the body, the desired velocity may never even be reached (a more complicated force equation would be needed, which would have extra parameters and its own problems).
Joint motors solve all these problems: they bring the body up to speed in one time step, provided that does not take more force than is allowed. Joint motors need no extra parameters because they are actually implemented as constraints. They can effectively see one time step into the future to work out the correct force. This makes joint motors more computationally expensive than computing the forces yourself, but they are much more robust and stable, and far less time consuming to design with. This is especially true with larger rigid body systems.
Similar arguments apply to joint stops.
Parameter Functions
Here are the functions that set stop and motor parameters (as well as other kinds of parameters) on a joint:
void dJointSetHingeParam (dJointID, int parameter, dReal value); void dJointSetSliderParam (dJointID, int parameter, dReal value); void dJointSetHinge2Param (dJointID, int parameter, dReal value); void dJointSetUniversalParam (dJointID, int parameter, dReal value); void dJointSetAMotorParam (dJointID, int parameter, dReal value); void dJointSetLMotorParam (dJointID, int parameter, dReal value); void dJointSetPRParam (dJointID, int parameter, dReal value); void dJointSetPUParam (dJointID, int parameter, dReal value); void dJointSetPistonParam (dJointID, int parameter, dReal value); void dJointSetDBallParam(dJointID, int parameter, dReal value); void dJointSetDHingeParam(dJointID, int parameter, dReal value); void dJointSetTransmissionParam(dJointID, int parameter, dReal value); dReal dJointGetHingeParam (dJointID, int parameter); dReal dJointGetSliderParam (dJointID, int parameter); dReal dJointGetHinge2Param (dJointID, int parameter); dReal dJointGetUniversalParam (dJointID, int parameter); dReal dJointGetAMotorParam (dJointID, int parameter); dReal dJointGetLMotorParam (dJointID, int parameter); dReal dJointGetPRParam (dJointID, int parameter); dReal dJointGetPUParam (dJointID, int parameter); dReal dJointGetPistonParam (dJointID, int parameter); dReal dJointGetDBallParam(dJointID, int parameter); dReal dJointGetDHingeParam(dJointID, int parameter); dReal dJointGetTransmissionParam(dJointID, int parameter);
Set/get limit/motor parameters for each joint type. The parameter numbers are:
| dParamLoStop |
Low stop angle or position. Setting this to -dInfinity (the default value) turns off the low stop. For rotational joints, this stop must be greater than - pi to be effective. |
| dParamHiStop | High stop angle or position. Setting this to dInfinity (the default value) turns off the high stop. For rotational joints, this stop must be less than pi to be effective. If the high stop is less than the low stop then both stops will be ineffective. |
| dParamVel | Desired motor velocity (this will be an angular or linear velocity). |
| dParamFMax | The maximum force or torque that the motor will use to achieve the desired velocity. This must always be greater than or equal to zero. Setting this to zero (the default value) turns off the motor. |
| dParamFudgeFactor | The current joint stop/motor implementation has a small problem: when the joint is at one stop and the motor is set to move it away from the stop, too much force may be applied for one time step, causing a jumping motion. This fudge factor is used to scale this excess force. It should have a value between zero and one (the default value). If the jumping motion is too visible in a joint, the value can be reduced. Making this value too small can prevent the motor from being able to move the joint away from a stop. |
| dParamBounce | The bouncyness of the stops. This is a restitution parameter in the range 0..1. 0 means the stops are not bouncy at all, 1 means maximum bouncyness. |
| dParamCFM | The constraint force mixing (CFM) value used when not at a stop. |
| dParamStopERP | The error reduction parameter (ERP) used by the stops. |
| dParamStopCFM | The constraint force mixing (CFM) value used by the stops. Together with the ERP value this can be used to get spongy or soft stops. Note that this is intended for unpowered joints, it does not really work as expected when a powered joint reaches its limit. |
| dParamSuspensionERP | Suspension error reduction parameter (ERP). Currently this is only implemented on the hinge-2 joint. |
| dParamSuspensionCFM | Suspension constraint force mixing (CFM) value. Currently this is only implemented on the hinge-2 joint. |
If a particular parameter is not implemented by a given joint, setting it will have no effect and getting it will return 0.
Important: These parameter names can be optionally followed by a digit (2 or 3) to indicate the second or third set of parameters, e.g. for the second axis in a hinge-2 joint, or the third axis in an AMotor joint. A constant dParamGroup is also defined such that: dParamXi = dParamX + dParamGroup * (i-1)
The following table shows the valid parameter groups for each joint type.
| Joint Type | Number of Param Groups |
| Ball And Socket | 0 |
| Hinge | 1 |
| Slider | 1 |
| Contact | 0 |
| Universal | 2 |
| Fixed | 0 |
| Angular Motor | 3 |
| Linear Motor | 3 |
| Plane2D | 3 |
| Rotoide and Prismatic | 0 |
Setting Joint Torques/Forces Directly
Motors (see above) allow you to set joint velocities directly. However, you may instead wish to set the torque or force at a joint instead. These functions do just that. Note that they don't affect the motor, but simply call dBodyAddForce dBodyAddTorque on the bodies attached to it.
void dJointAddHingeTorque (dJointID, dReal torque);
Applies the torque about the hinge axis. That is, it applies a torque with magnitude torque, in the direction of the hinge axis, to body 1, and with the same magnitude but in opposite direction to body 2. This function is just a wrapper for dBodyAddTorque.
void dJointAddUniversalTorques (dJointID, dReal torque1, dReal torque2);
Applies torque1 about the universal's axis 1, and torque2 about the universal's axis 2. This function is just a wrapper for dBodyAddTorque.
void dJointAddSliderForce (dJointID, dReal force);
Applies the given force in the slider's direction. That is, it applies a force with magnitude force, in the direction slider's axis, to body1, and with the same magnitude but opposite direction to body2. This function is just a wrapper for dBodyAddForce.
void dJointAddHinge2Torques (dJointID, dReal torque1, dReal torque2);
Applies torque1 about the hinge2's axis 1, and torque2 about the hinge2's axis 2. This function is just a wrapper for dBodyAddTorque.
void dJointAddAMotorTorques (dJointID, dReal torque0, dReal torque1, dReal torque2);
Applies torque0 about the AMotor's axis 0, torque1 about the AMotor's axis 1, and torque2 about the AMotor's axis 2. If the motor has fewer than three axes, the higher torques are ignored. This function is just a wrapper for dBodyAddTorque.
Support Functions
Initialization
void dInitODE (); int dInitODE2 (unsigned InitFlags); void dCloseODE ();
Perform library initialization.
- dInitODE2() must be called before the library's first use. InitFlags can be either zero or dInitFlagManualThreadCleanup. It must be called only once until dCloseODE() is called.
- dInitODE() is a short hand for:
dInitODE2(0);
dAllocateODEDataForThread(dAllocateMaskAll);
- dCloseODE() performs library cleanup. After that, dInitODE2() must be called before ODE can be used again. Use it only if you are going to use ODE from a single thread.
int dAllocateODEDataForThread (unsigned AllocateFlags); void dCleanupODEAllDataForThread ();
- dAllocateODEDataForThread() must be called from every thread that will use ODE. AllocateFlags can be either zero or dAllocateFlagCollisionData.
- Use dCleanupODEAllDataForThread () only if the library was initialized with dInitFlagManualThreadCleanup.
Configuration
const char* dGetConfiguration ();
Returns the specific ODE build configuration as a string of tokens. The string can be parsed in a similar way to the OpenGL extension mechanism, the naming convention should be familiar too. The following extensions are reported:
- ODE
- ODE_single_precision
- ODE_double_precision
- ODE_EXT_no_debug
- ODE_EXT_trimesh
- ODE_EXT_opcode
- ODE_EXT_gimpact
- ODE_EXT_malloc_not_alloca
- ODE_OPC_16bit_indices
- ODE_OPC_new_collider
int dCheckConfiguration ( const char* token );
Helper to check for a token in the ODE configuration string. Caution, this function is case sensitive.
Rotation functions
Rigid body orientations are represented with unit quaternions. It consists of four numbers, [math]\displaystyle{ [w, x, y, z] }[/math], where:
- [math]\displaystyle{ w = \cos( \theta / 2) }[/math]
- [math]\displaystyle{ (x, y, z) = \vec{u} \sin( \theta /2) }[/math]
- [math]\displaystyle{ \theta }[/math] is a rotation angle
- [math]\displaystyle{ \vec{u} }[/math] is a unit length rotation axis.
Every rigid body also has a 3x3 rotation matrix that is derived from the quaternion; quaternions are convenient for dynamics calculations, but matrices are better for linear transformations. The rotation matrix and the quaternion always match. Geoms have only rotation matrices, as they are not involved in dynamics. Quaternions are the preferred method of transmitting rotations between libraries (e.g. to/from 3D engines), as there are only 2 conventions ([w, x, y, z] and [x, y, z, w]) that are easy to notice when swapped; similarly, Euler angles are undesirable, as there are too many possible conventions, making two independent implementations unlikely to match.
Some information about quaternions:
- q and -q represent the same rotation.
- The inverse of a quaternion
[w, x, y, z]is[w, -x, -y, -z].
The following are utility functions for dealing with rotation matrices and quaternions.
void dRSetIdentity (dMatrix3 R);
Set R to the identity matrix (i.e. no rotation).
void dRFromAxisAndAngle (dMatrix3 R, dReal ax, dReal ay, dReal az, dReal angle);
Compute the rotation matrix R as a rotation of angle radians along the axis (ax,ay,az).
void dRFromEulerAngles (dMatrix3 R, dReal phi, dReal theta, dReal psi);
Compute the rotation matrix R from the three Euler rotation angles.
void dRFrom2Axes (dMatrix3 R, dReal ax, dReal ay, dReal az, dReal bx, dReal by, dReal bz);
Compute the rotation matrix R from the two vectors a = [ax, ay, az] and b = [bx, by, bz]. a and b are the desired [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] axes of the rotated coordinate system. If necessary, both vectors will be normalized, and b will be projected so that it is perpendicular to a. The desired [math]\displaystyle{ z }[/math] axis is the cross product [math]\displaystyle{ a \times b }[/math].
void dQSetIdentity (dQuaternion q);
Set q to the identity rotation (i.e. no rotation).
void dQFromAxisAndAngle (dQuaternion q, dReal ax, dReal ay, dReal az, dReal angle);
Compute q as a rotation of angle radians along the axis (ax,ay,az).
void dQMultiply0 (dQuaternion qa, const dQuaternion qb, const dQuaternion qc); void dQMultiply1 (dQuaternion qa, const dQuaternion qb, const dQuaternion qc); void dQMultiply2 (dQuaternion qa, const dQuaternion qb, const dQuaternion qc); void dQMultiply3 (dQuaternion qa, const dQuaternion qb, const dQuaternion qc);
Set qa = qb*qc. This is that same as qa = rotation qc followed by rotation qb. The 0/1/2/3 versions use inverse of arguments: 0 inverts nothing, 1 uses the inverse of qb, and 2 uses the inverse of qc. Option 3 uses the inverse of both.
void dQtoR (const dQuaternion q, dMatrix3 R);
Convert quaternion q to rotation matrix R.
void dRtoQ (const dMatrix3 R, dQuaternion q);
Convert rotation matrix R to quaternion q.
void dWtoDQ (const dVector3 w, const dQuaternion q, dVector4 dq);
Given an existing orientation q and an angular velocity vector w, return in dq the resulting [math]\displaystyle{ \operatorname{d}q/\operatorname{d}t }[/math].
Mass functions
The mass parameters of a rigid body are described by a dMass structure:
typedef struct dMass {
dReal mass; // total mass of the rigid body
dVector3 c; // center of gravity position in body frame (x,y,z)
dMatrix3 I; // 3x3 inertia tensor in body frame, about POR
} dMass;
The following functions operate on this structure:
void dMassSetZero (dMass *);
Set all the mass parameters to zero.
void dMassSetParameters (dMass *, dReal themass,
dReal cgx, dReal cgy, dReal cgz,
dReal I11, dReal I22, dReal I33,
dReal I12, dReal I13, dReal I23);
Set the mass parameters to the given values. themass is the mass of the body. (cx,cy,cz) is the center of gravity position in the body frame. The Ixx values are the elements of the inertia matrix: ( I11 I12 I13 ) ( I12 I22 I23 ) ( I13 I23 I33 )
void dMassSetSphere (dMass *, dReal density, dReal radius); void dMassSetSphereTotal (dMass *, dReal total_mass, dReal radius);
Set the mass parameters to represent a sphere of the given radius and density, with the center of mass at (0,0,0) relative to the body. The first function accepts the density of the sphere, the second accepts the total mass of the sphere.
void dMassSetCapsule (dMass *, dReal density, int direction, dReal radius, dReal length); void dMassSetCapsuleTotal (dMass *, dReal total_mass, int direction, dReal radius, dReal length);
Set the mass parameters to represent a capsule of the given parameters and density, with the center of mass at (0,0,0) relative to the body. The radius of the cylinder (and the spherical cap) is radius. The length of the cylinder (not counting the spherical cap) is length. The cylinder's long axis is oriented along the body's x, y or z axis according to the value of direction (1=x, 2=y, 3=z). The first function accepts the density of the object, the second accepts its total mass.
void dMassSetCylinder (dMass *, dReal density, int direction, dReal radius, dReal length); void dMassSetCylinderTotal (dMass *, dReal total_mass, int direction, dReal radius, dReal length);
Set the mass parameters to represent a flat-ended cylinder of the given parameters and density, with the center of mass at (0,0,0) relative to the body. The radius of the cylinder is radius. The length of the cylinder is length. The cylinder's long axis is oriented along the body's x, y or z axis according to the value of direction (1=x, 2=y, 3=z). The first function accepts the density of the object, the second accepts its total mass.
void dMassSetBox (dMass *, dReal density, dReal lx, dReal ly, dReal lz); void dMassSetBoxTotal (dMass *, dReal total_mass, dReal lx, dReal ly, dReal lz);
Set the mass parameters to represent a box of the given dimensions and density, with the center of mass at (0,0,0) relative to the body. The side lengths of the box along the x, y and z axes are lx, ly and lz. The first function accepts the density of the object, the second accepts its total mass.
void dMassSetTrimesh (dMass *, dReal density, dGeomID g)
Set the mass parameters to represent an arbitrary trimesh of the given geometry and density, location of a trimesh geometry center of mass and set the inertia matrix.
void dMassAdjust (dMass *, dReal newmass);
Given mass parameters for some object, adjust them so the total mass is now newmass. This is useful when using the above functions to set the mass parameters for certain objects - they take the object density, not the total mass.
void dMassTranslate (dMass *, dReal x, dReal y, dReal z);
Given mass parameters for some object, adjust them to represent the object displaced by (x,y,z) relative to the body frame.
void dMassRotate (dMass *, const dMatrix3 R);
Given mass parameters for some object, adjust them to represent the object rotated by R relative to the body frame.
void dMassAdd (dMass *a, const dMass *b);
Add the mass b to the mass a.
Math functions
(There are quite a lot of these, but they're not standardized enough to document yet).
Export functions
Functions used to print the state of a world.
void dWorldExportDIF (dWorldID w, FILE *file, const char *prefix)
Set file to a file descriptor to print to a file or to stdout to print to the standard output (console).
Error and memory functions
The following is taken directly from ode/error.h, version .11:
All user defined error functions have this type. error and debug functions should not return:
typedef void dMessageFunction (int errnum, const char *msg, va_list ap);
Set a new error, debug or warning handler. if fn is 0, the default handlers are used:
void dSetErrorHandler (dMessageFunction *fn); void dSetDebugHandler (dMessageFunction *fn); void dSetMessageHandler (dMessageFunction *fn);
Return the current error, debug or warning handler. if the return value is 0, the default handlers are in place:
dMessageFunction *dGetErrorHandler(void); dMessageFunction *dGetDebugHandler(void); dMessageFunction *dGetMessageHandler(void);
Generate a fatal error, debug trap or a message:
ODE_API void dError (int num, const char *msg, ...); ODE_API void dDebug (int num, const char *msg, ...); ODE_API void dMessage (int num, const char *msg, ...);
Collision Detection
ODE has two main components: a dynamics simulation engine and a collision detection engine. The collision engine is given information about the shape of each body. At each time step it figures out which bodies touch each other and passes the resulting contact point information to the user. The user in turn creates contact joints between bodies.
Using ODE's collision detection is optional -- an alternative collision detection system can be used as long as it can supply the right kinds of contact information.
Collision tests supported
Here is a table of what primitives collide with which other, ordered by object complexity (information taken from collision_kernel.cpp->initColliders() function).
| Ray | Plane | Sphere | Box | Capsule | Cylinder | Trimesh | Convex | Heightfield | |
|---|---|---|---|---|---|---|---|---|---|
| Ray | No[2] | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Plane | - | No[2] | Yes | Yes | Yes | Yes | Yes | Yes | No[2] |
| Sphere | - | - | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Box | - | - | - | Yes | Yes | Yes | Yes | Yes[3] | Yes |
| Capsule | - | - | - | - | Yes | Yes[3] | Yes | Yes[3] | Yes |
| Cylinder | - | - | - | - | - | Yes[3] | Yes | Yes[3] | Yes |
| Trimesh | - | - | - | - | - | - | Yes | No | Yes |
| Convex | - | - | - | - | - | - | - | Yes | Yes |
| Heightfield | - | - | - | - | - | - | - | - | No[2] |
Note 1: This feature exists only in a recent SVN revision and has not yet been added to an official release.
Note 2: Not planned to be implemented, since this collision combination doesn't make much sense in a physics simulation.
Note 3: By enabling the libccd colliders.
It's possible to override the collision handler for a certain pair of geom classes through dSetColliderOverride():
void dSetColliderOverride (int class1, int class2, dColliderFn *fn);
dColliderFn is defined as:
typedef int dColliderFn (dGeomID o1, dGeomID o2, int flags, dContactGeom *contact, int skip);
Contact points
If two bodies touch, or if a body touches a static feature in its environment, the contact is represented by one or more "contact points". Each contact point has a corresponding dContactGeom structure:
struct dContactGeom {
dVector3 pos; // contact position
dVector3 normal; // normal vector
dReal depth; // penetration depth
dGeomID g1,g2; // the colliding geoms
};
posrecords the contact position, in global coordinates.
depthis the depth to which the two bodies inter-penetrate each other. If the depth is zero then the two bodies have a grazing contact, i.e. they "only just" touch. However, this is rare - the simulation is not perfectly accurate and will often step the bodies too far so that the depth is nonzero.
normalis a unit length vector that is, generally speaking, perpendicular to the contact surface.
g1andg2are the geometry objects that collided.
The convention is that if body 1 is moved along the normal vector by a distance depth (or equivalently if body 2 is moved the same distance in the opposite direction) then the contact depth will be reduced to zero. This means that the normal vector points "in" to body 1.
In real life, contact between two bodies is a complex thing. Representing contacts by contact points is only an approximation. Contact "patches" or "surfaces" might be more physically accurate, but representing these things in high speed simulation software is a challenge.
Each extra contact point added to the simulation will slow it down some more, so sometimes we are forced to ignore contact points in the interests of speed. For example, when two boxes collide many contact points may be needed to properly represent the geometry of the situation, but we may choose to keep only the best three. Thus we are piling approximation on top of approximation.
Contact points can then be used, for example, to generate contact joints.
Geoms
Geometry objects (or "geoms" for short) are the fundamental objects in the collision system. A geom can represents a single rigid shape (such as a sphere or box), or it can represents a group of other geoms - this is a special kind of geom called a "space".
Any geom can be collided against any other geom to yield zero or more contact points. Spaces have the extra capability of being able to collide their contained geoms together to yield internal contact points.
Geoms can be placeable or non-placeable. A placeable geom has a position vector and a 3*3 rotation matrix, just like a rigid body, that can be changed during the simulation. A non-placeable geom does not have this capability - for example, it may represent some static feature of the environment that can not be moved. Spaces are non-placeable geoms, because each contained geom may have its own position and orientation but it does not make sense for the space itself to have a position and orientation.
To use the collision engine in a rigid body simulation, placeable geoms are associated with rigid body objects. This allows the collision engine to get the position and orientation of the geoms from the bodies. Note that geoms are distinct from rigid bodies in that a geom has geometrical properties (size, shape, position and orientation) but no dynamical properties (such as velocity or mass). A body and a geom together represent all the properties of the simulated object.
Every geom is an instance of a class, such as sphere, plane, or box. There are a number of built-in classes, described below, and you can define your own classes as well.
The point of reference of a placeable geoms is the point that is controlled by its position vector. The point of reference for the standard classes usually corresponds to the geom's center of mass. This feature allows the standard classes to be easily connected to dynamics bodies. If other points of reference are required, a transformation object can be used to encapsulate a geom.
The concepts and functions that apply to all geoms will be described below, followed by the various geometry classes and the functions that manipulate them.
Spaces
A space is a non-placeable geom that can contain other geoms. It is similar to the rigid body concept of the "world", except that it applies to collision instead of dynamics.
Space objects exist to make collision detection go faster. Without spaces, you might generate contacts in your simulation by calling dCollide to get contact points for every single pair of geoms. For N geoms this is O(N2) tests, which is too computationally expensive if your environment has many objects.
A better approach is to insert the geoms into a space and call dSpaceCollide. The space will then perform collision culling, which means that it will quickly identify which pairs of geoms are potentially intersecting. Those pairs will be passed to a callback function, which can in turn call dCollide on them. This saves a lot of time that would have been spent in useless dCollide tests, because the number of pairs passed to the callback function will be a small fraction of every possible object-object pair.
Spaces can contain other spaces. This is useful for dividing a collision environment into several hierarchies to further optimize collision detection speed. This will be described in more detail below.
General geom functions
The following functions can be applied to any geom.
void dGeomDestroy (dGeomID);
Destroy a geom, removing it from any space it is in first. This one function destroys a geom of any type, but to create a geom you must call a creation function for that type.
When a space is destroyed, if its cleanup mode is 1 (the default) then all the geoms in that space are automatically destroyed as well.
void dGeomSetData (dGeomID, void *); void * dGeomGetData (dGeomID);
These functions set and get the user-defined data pointer stored in the geom.
void dGeomSetBody (dGeomID, dBodyID); dBodyID dGeomGetBody (dGeomID);
These functions set and get the body associated with a placeable geom. Setting a body on a geom automatically combines the position vector and rotation matrix of the body and geom, so that setting the position or orientation of one will set the value for both objects.
Setting a body ID of zero gives the geom its own position and rotation, independent from any body. If the geom was previously connected to a body then its new independent position/rotation is set to the current position/rotation of the body.
Calling these functions on a non-placeable geom results in a runtime error in the debug build of ODE.
void dGeomSetPosition (dGeomID, dReal x, dReal y, dReal z); void dGeomSetRotation (dGeomID, const dMatrix3 R); void dGeomSetQuaternion (dGeomID, const dQuaternion);
Set the position vector, rotation matrix or quaternion of a placeable geom. These functions are analogous to dBodySetPosition, dBodySetRotation and dBodySetQuaternion. If the geom is attached to a body, the body's position / rotation / quaternion will also be changed.
Calling these functions on a non-placeable geom results in a runtime error in the debug build of ODE.
const dReal * dGeomGetPosition (dGeomID); const dReal * dGeomGetRotation (dGeomID); void dGeomGetQuaternion (dGeomID, dQuaternion result);
The first two return pointers to the geom's position vector and rotation matrix. The returned values are pointers to internal data structures, so the vectors are valid until any changes are made to the geom. If the geom is attached to a body, the body's position / rotation pointers will be returned, i.e. the result will be identical to calling dBodyGetPosition or dBodyGetRotation.
dGeomGetQuaternion copies the geom's quaternion into the space provided. If the geom is attached to a body, the body's quaternion will be returned, i.e. the resulting quaternion will be the same as the result of calling dBodyGetQuaternion.
Calling these functions on a non-placeable geom results in a runtime error in the debug build of ODE.
void dGeomSetOffsetPosition (dGeomID, dReal x, dReal y, dReal z); void dGeomSetOffsetRotation (dGeomID, const dMatrix3 R); void dGeomSetOffsetQuaternion (dGeomID, const dQuaternion Q);
Set the offset position, rotation or quaternion of a geom. The geom must be attached to a body. If the geom did not have an offset, it is automatically created. This sets up an additional (local) transformation for the geom, since geoms attached to a body share their global position and rotation. To disable the offset call dGeomClearOffset.
void dGeomSetOffsetWorldPosition (dGeomID, dReal x, dReal y, dReal z); void dGeomSetOffsetWorldRotation (dGeomID, const dMatrix3 R); void dGeomSetOffsetWorldQuaternion (dGeomID, const dQuaternion Q);
Set the offset world position, rotation or quaternion of a geom. The new local offset is the difference of the current body transformation, so that the geom is placed and oriented in the world as specified, without changing the body's transformation. See also the previous three offset functions.
const dReal * dGeomGetOffsetPosition (dGeomID); const dReal * dGeomGetOffsetRotation (dGeomID); void dGeomGetOffsetQuaternion (dGeomID, dQuaternion result);
Get the offset position, rotation or quaternion of a geom. The returned value of the first two functions are pointers to the geom's internal data structure. They are valid until any changes are made to the geom. If the geom has no offset the zero vector is returned, in case of dGeomGetOffsetQuaternion the identity quaternion is returned.
void dGeomClearOffset (dGeomID);
Disable the geom's offset. The geom will be repositioned / oriented at the body's position / orientation. If the geom has no offset, this function does nothing. Note, that this will eliminate the offset and is more efficient than setting the offset to the identity transformation.
void dGeomGetAABB (dGeomID, dReal aabb[6]);
Return in aabb an axis aligned bounding box that surrounds the given geom. The aabb array has elements (minx, maxx, miny, maxy, minz, maxz). If the geom is a space, a bounding box that surrounds all contained geoms is returned.
This function may return a pre-computed cached bounding box, if it can determine that the geom has not moved since the last time the bounding box was computed.
int dGeomIsSpace (dGeomID);
Return 1 if the given geom is a space, or 0 if not.
dSpaceID dGeomGetSpace (dGeomID);
Return the space that the given geometry is contained in, or return 0 if it is not contained in any space.
int dGeomGetClass (dGeomID);
Given a geom, this returns its class number. The standard class numbers are:
| dSphereClass = 0 | Sphere |
| dBoxClass | Box |
| dCapsuleClass | Capsule (i.e. cylinder with half-sphere caps at its ends) |
| dCylinderClass | Regular flag ended Cylinder |
| dPlaneClass | Infinite plane (non-placeable) |
| dRayClass | Ray |
| dConvexClass | |
| dGeomTransformClass | Geometry transform |
| dTriMeshClass | Triangle mesh |
| dHeightfieldClass | |
| dFirstSpaceClass | |
| dSimpleSpaceClass = dFirstSpaceClass | Simple space |
| dHashSpaceClass | Hash table based space |
| dQuadTreeSpaceClass | Quad tree based space |
| dLastSpaceClass = dQuadTreeSpaceClass | |
| dFirstUserClass | |
| dLastUserClass = dFirstUserClass + dMaxUserClasses - 1, |
The class value is equal to value of the previous row + 1, if there is no equal sign.
User defined classes will return their own numbers.
void dGeomSetCategoryBits (dGeomID, unsigned long bits); void dGeomSetCollideBits (dGeomID, unsigned long bits); unsigned long dGeomGetCategoryBits (dGeomID); unsigned long dGeomGetCollideBits (dGeomID);
Set and get the "category" and "collide" bitfields for the given geom. These bitfields are use by spaces to govern which geoms will interact with each other. The bit fields are guaranteed to be at least 32 bits wide. The default category and collide values for newly created geoms have all bits set.
void dGeomEnable (dGeomID); void dGeomDisable (dGeomID); int dGeomIsEnabled (dGeomID);
Enable and disable a geom. Disabled geoms are completely ignored by dSpaceCollide and dSpaceCollide2, although they can still be members of a space.
dGeomIsEnabled() returns 1 if a geom is enabled or 0 if it is disabled. New geoms are created in the enabled state.
Collision detection
A collision detection "world" is created by making a space and then adding geoms to that space. At every time step we want to generate a list of contacts for all the geoms that intersect each other. Three functions are used to do this:
- dCollide intersects two geoms and generates contact points.
- dSpaceCollide determines which pairs of geoms in a space may potentially intersect, and calls a callback function with each candidate pair. This does not generate contact points directly, because the user may want to handle some pairs specially - for example by ignoring them or using different contact generating strategies. Such decisions are made in the callback function, which can choose whether or not to call dCollide for each pair.
- dSpaceCollide2 determines which geoms from one space may potentially intersect with geoms from another space, and calls a callback function with each candidate pair. It can also test a single non-space geom against a space or treat a space of lower inclusion sublevel as a geom against a space of higher level. This function is useful when there is a collision hierarchy, i.e. when there are spaces that contain other spaces.
The collision system has been designed to give the user maximum flexibility to decide which objects will be tested against each other. This is why there are three collision functions instead of, for example, one function that just generates all the contact points.
Spaces may contain other spaces. These sub-spaces will typically represent a collection of geoms (or other spaces) that are located near each other. This is useful for gaining extra collision performance by dividing the collision world into hierarchies. Here is an example of where this is useful:
Suppose you have two cars driving over some terrain. Each car is made up of many geoms. If all these geoms were inserted into the same space, the collision computation time between the two cars would always be proportional to the total number of geoms (or even to the square of this number, depending on which space type is used).
To speed up collision a separate space is created to represent each car. The car geoms are inserted into the car-spaces, and the car-spaces are inserted into the top level space. At each time step dSpaceCollide is called for the top level space. This will do a single intersection test between the car-spaces (actually between their bounding boxes) and call the callback if they touch. The callback can then test the geoms in the car-spaces against each other using dSpaceCollide2. If the cars are not near each other then the callback is not called and no time is wasted performing unnecessary tests.
If space hierarchies are being used then the callback function may be called recursively, e.g. if dSpaceCollide calls the callback which in turn calls dSpaceCollide with the same callback function. In this case the user must make sure that the callback function is properly reentrant.
Here is a sample callback function that traverses through all spaces and sub-spaces, generating all possible contact points for all intersecting geoms:
void nearCallback (void *data, dGeomID o1, dGeomID o2)
{
if (dGeomIsSpace (o1) || dGeomIsSpace (o2)) {
// colliding a space with something :
dSpaceCollide2 (o1, o2, data,&nearCallback);
// collide all geoms internal to the space(s)
if (dGeomIsSpace (o1))
dSpaceCollide ((dSpaceID)o1, data, &nearCallback);
if (dGeomIsSpace (o2))
dSpaceCollide ((dSpaceID)o2, data, &nearCallback);
} else {
// colliding two non-space geoms, so generate contact
// points between o1 and o2
int num_contact = dCollide (o1, o2, max_contacts,contact_array, skip);
// add these contact points to the simulation ...
}
}
... // collide all objects together
dSpaceCollide (top_level_space,0,&nearCallback);
A space callback function is not allowed to modify a space while that space is being processed with dSpaceCollide or dSpaceCollide2. For example, you can not add or remove geoms from a space, and you can not reposition the geoms within a space. Doing so will trigger a runtime error in the debug build of ODE.
Category and Collide Bitfields
Each geom has a "category" and "collide" bitfield that can be used to assist the space algorithms in determining which geoms should interact and which should not. Use of this feature is optional - by default geoms are considered to be capable of colliding with any other geom.
Each bit position in the bitfield represents a different category of object. The actual meaning of these categories (if any) is user defined. The category bitfield indicates which categories a geom is a member of. The collide bitfield indicates which categories the geom will collide with during collision detection.
A pair of geoms will be considered by dSpaceCollide and dSpaceCollide2 for passing to the callback only if one of them has a collide bit set that corresponds to a category bit in the other. The exact test is as follows:
// test if geom o1 and geom o2 can collide
cat1 = dGeomGetCategoryBits (o1);
cat2 = dGeomGetCategoryBits (o2);
col1 = dGeomGetCollideBits (o1);
col2 = dGeomGetCollideBits (o2);
if ((cat1 & col2) || (cat2 & col1)) {
// call the callback with o1 and o2
} else {
// do nothing, o1 and o2 do not collide
}
Note that only dSpaceCollide and dSpaceCollide2 use these bitfields, they are ignored by dCollide.
Typically a geom will belong only to a single category, so only one bit will be set in the category bitfield. The bitfields are guaranteed to be at least 32 bits wide, so the user is able to specify an arbitrary pattern of interactions for up to 32 objects. If there are more than 32 objects then some of them will obviously have to have the same category.
Sometimes the category field will contain multiple bits set, e.g. if the geom is a space them you may want to set the category to the union of all the geom categories that are contained.
Design note: Why don't we just have a single category bitfield and use the test (cat1 & cat2) ? This is simpler, but a single field requires more bits to represent some patterns of interaction. For example, if 32 geoms have an interaction pattern that is a 5 dimensional hypercube, 80 bit are required in the simpler scheme. The simpler scheme also makes it harder to determine what the categories should be for some situations.
Collision Detection Functions
int dCollide (dGeomID o1, dGeomID o2, int flags, dContactGeom *contact, int skip);
Given two geoms o1 and o2 that potentially intersect, generate contact information for them. Internally, this just calls the correct class-specific collision functions for o1 and o2.
flags specifies how contacts should be generated if the geoms touch.
The lower 16 bits of flags is an integer that specifies the maximum number of contact points to generate. The number of contacts requested can't be zero.
The higher 16 bits of flags can contain any combination of the following flags:
- CONTACTS_UNIMPORTANT - just generate any contacts (skip any contact improvements and return any contacts found as soon as possible).
All other bits in flags must be zeroed. In the future the other bits may be used to select from different contact generation strategies.
contact points to an array of dContactGeom structures. The array must be able to hold at least the maximum number of contacts. These dContactGeom structures may be embedded within larger structures in the array - the skip parameter is the byte offset from one dContactGeom to the next in the array. If skip is sizeof(dContactGeom) then contact points to a normal (C-style) array. It is an error for skip to be smaller than sizeof(dContactGeom).
If the geoms intersect, this function returns the number of contact points generated (and updates the contact array), otherwise it returns 0 (and the contact array is not touched).
If a space is passed as o1 or o2 then this function will collide all objects contained in o1 with all objects contained in o2, and return the resulting contact points. This method for colliding spaces with geoms (or spaces with spaces) provides no user control over the individual collisions. To get that control, use dSpaceCollide or dSpaceCollide2 instead.
If o1 and o2 are the same geom then this function will do nothing and return 0. Technically speaking an object intersects with itself, but it is not useful to find contact points in this case.
This function does not care if o1 and o2 are in the same space or not (or indeed if they are in any space at all).
void dSpaceCollide (dSpaceID space, void *data, dNearCallback *callback);
This determines which pairs of geoms in a space may potentially intersect, and calls the callback function with each candidate pair. The callback function is of type dNearCallback, which is defined as:
typedef void dNearCallback (void *data, dGeomID o1, dGeomID o2);
The data argument is passed from dSpaceCollide directly to the callback function. Its meaning is user defined. The o1 and o2 arguments are the geoms that may be near each other.
The callback function can call dCollide on o1 and o2 to generate contact points between each pair. Then these contact points may be added to the simulation as contact joints. The user's callback function can of course chose not to call dCollide for any pair, e.g. if the user decides that those pairs should not interact.
Other spaces that are contained within the colliding space are not treated specially, i.e. they are not recursed into. The callback function may be passed these contained spaces as one or both geom arguments.
dSpaceCollide() is guaranteed to pass all intersecting geom pairs to the callback function, but it may also make mistakes and pass non-intersecting pairs. The number of mistaken calls depends on the internal algorithms used by the space. Thus you should not expect that dCollide will return contacts for every pair passed to the callback.
void dSpaceCollide2 (dGeomID o1, dGeomID o2, void *data, dNearCallback *callback);
This function is similar to dSpaceCollide, except that it is passed two geoms (or spaces) as arguments. It calls the callback for all potentially intersecting pairs that contain one geom from o1 and one geom from o2.
The exact behavior depends on the types of o1 and o2:
- If one argument is a non-space geom and the other is a space, the callback is called with all potential intersections between the geom and the objects in the space.
- If both arguments are spaces and their sublevel values differ, the space with lower sublevel is treated as a geom against the space of higher sublevel (sublevel value can be assigned to a space with
dSpaceSetSublevelcall - the value is not tracked automatically!). - If both
o1ando2are spaces of the same sublevel then this calls the callback for all potentially intersecting pairs that contain one geom fromo1and one geom fromo2. The algorithm that is used depends on what kinds of spaces are being collided. If no optimized algorithm can be selected then this function will resort to one of the following two strategies: - All the geoms in
o1are tested one-by-one againsto2. - All the geoms in
o2are tested one-by-one againsto1. The strategy used may depend on a number of rules, but in general the space with less objects has its geoms examined one-by-one. - If both arguments are the same space, this is equivalent to calling
dSpaceCollideon that space. - If both arguments are non-space geoms, this simply calls the callback once with these arguments. If this function is given a space and an geom X in that same space, this case is not treated specially. In this case the callback will always be called with the pair (X,X), because an objects always intersects with itself. The user may either test for this case and ignore it, or just pass the pair (X,X) to dCollide (which will be guaranteed to return 0).
Space functions
There are several kinds of spaces. Each kind uses different internal data structures to store the geoms, and different algorithms to perform the collision culling:
- Simple space. This does not do any collision culling - it simply checks every possible pair of geoms for intersection, and reports the pairs whose AABBs overlap. The time required to do intersection testing for n objects is O(n2). This should not be used for large numbers of objects, but it can be the preferred algorithm for a small number of objects. This is also useful for debugging potential problems with the collision system.
- Multi-resolution hash table space. This uses an internal data structure that records how each geom overlaps cells in one of several three dimensional grids. Each grid has cubical cells of side lengths 2i, where i is an integer that ranges from a minimum to a maximum value. The time required to do intersection testing for n objects is O(n) (as long as those objects are not clustered together too closely), as each object can be quickly paired with the objects around it.
- Quadtree space. This uses a pre-allocated hierarchical grid-based AABB tree to quickly cull collision checks. It's exceptionally quick for large amounts of objects in landscape-shaped worlds. The amount of memory used is 4^depth * 32 bytes. Currently dSpaceGetGeom is not implemented for the quadtree space.
Here are the functions used for spaces:
dSpaceID dSimpleSpaceCreate (dSpaceID space); dSpaceID dHashSpaceCreate (dSpaceID space);
Create a space, either of the simple or multi-resolution hash table kind. If space is nonzero, insert the new space into that space.
dSpaceID dQuadTreeSpaceCreate (dSpaceID space, dVector3 Center, dVector3 Extents, int Depth);
Creates a quadtree space. center and extents define the size of the root block. depth sets the depth of the tree - the number of blocks that are created is 4^depth.
void dSpaceDestroy (dSpaceID);
This destroys a space. It functions exactly like dGeomDestroy except that it takes a dSpaceID argument. When a space is destroyed, if its cleanup mode is 1 (the default) then all the geoms in that space are automatically destroyed as well.
void dHashSpaceSetLevels (dSpaceID space, int minlevel, int maxlevel); void dHashSpaceGetLevels (dSpaceID space, int *minlevel, int *maxlevel);
Sets and get some parameters for a multi-resolution hash table space. The smallest and largest cell sizes used in the hash table will be 2^minlevel and 2^maxlevel respectively. minlevel must be less than or equal to maxlevel.
In dHashSpaceGetLevels the minimum and maximum levels are returned through pointers. If a pointer is zero then it is ignored and no argument is returned.
void dSpaceSetCleanup (dSpaceID space, int mode); int dSpaceGetCleanup (dSpaceID space);
Set and get the clean-up mode of the space. If the clean-up mode is 1, then the contained geoms will be destroyed when the space is destroyed. If the clean-up mode is 0 this does not happen. The default clean-up mode for new spaces is 1.
void dSpaceSetSublevel (dSpaceID space, int sublevel); int dSpaceGetSublevel (dSpaceID space);
Set and get sublevel value for the space. Sublevel affects how the space is handled in dSpaceCollide2 when it is collided with another space. If sublevels of both spaces match, the function iterates geometries of both spaces and collides them with each other. If sublevel of one space is greater than the sublevel of another one, only the geometries of the space with greater sublevel are iterated, another space is passed into collision callback as a geometry itself. By default all the spaces are assigned zero sublevel.
Note! The space sublevel IS NOT automatically updated when one space is inserted into another or removed from one. It is a client's responsibility to update sublevel value if necessary.
void dSpaceAdd (dSpaceID, dGeomID);
Add a geom to a space. This function can be called automatically if a space argument is given to a geom creation function.
void dSpaceRemove (dSpaceID, dGeomID);
Remove a geom from a space. This does nothing if the geom is not actually in the space. This function is called automatically by dGeomDestroy if the geom is in a space.
int dSpaceQuery (dSpaceID, dGeomID);
Return 1 if the given geom is in the given space, or return 0 if it is not.
int dSpaceGetNumGeoms (dSpaceID);
Return the number of geoms contained within a space.
dGeomID dSpaceGetGeom (dSpaceID, int i);
Return the i'th geom contained within the space. i must range from 0 to dSpaceGetNumGeoms()-1.
If any change is made to the space (including adding and deleting geoms) then no guarantee can be made about how the index number of any particular geom will change. Thus no space changes should be made while enumerating the geoms.
This function is guaranteed to be fastest when the geoms are accessed in the order 0,1,2,etc. Other non-sequential orders may result in slower access, depending on the internal implementation.
Geometry Classes
Sphere Class
dGeomID dCreateSphere (dSpaceID space, dReal radius);
Create a sphere geom of the given radius, and return its ID. If space is nonzero, insert it into that space. The point of reference for a sphere is its center.
void dGeomSphereSetRadius (dGeomID sphere, dReal radius);
Set the radius of the given sphere.
dReal dGeomSphereGetRadius (dGeomID sphere);
Return the radius of the given sphere.
dReal dGeomSpherePointDepth (dGeomID sphere, dReal x, dReal y, dReal z);
Return the depth of the point (x,y,z) in the given sphere. Points inside the geom will have positive depth, points outside it will have negative depth, and points on the surface will have zero depth.
Box Class
dGeomID dCreateBox (dSpaceID space, dReal lx, dReal ly, dReal lz);
Create a box geom of the given x/y/z side lengths (lx,ly,lz), and return its ID. If space is nonzero, insert it into that space. The point of reference for a box is its center.
void dGeomBoxSetLengths (dGeomID box, dReal lx, dReal ly, dReal lz);
Set the side lengths of the given box.
void dGeomBoxGetLengths (dGeomID box, dVector3 result);
Return in result the side lengths of the given box.
dReal dGeomBoxPointDepth (dGeomID box, dReal x, dReal y, dReal z);
Return the depth of the point (x,y,z) in the given box. Points inside the geom will have positive depth, points outside it will have negative depth, and points on the surface will have zero depth.
Plane Class
dGeomID dCreatePlane (dSpaceID space, dReal a, dReal b, dReal c, dReal d);
Create a plane geom of the given parameters, and return its ID. If space is nonzero, insert it into that space. The plane equation is
a*x+b*y+c*z = d The plane's normal vector is (a,b,c), and it must have length 1. Planes are non-placeable geoms. This means that, unlike placeable geoms, planes do not have an assigned position and rotation. This means that the parameters (a,b,c,d) are always in global coordinates. In other words it is assumed that the plane is always part of the static environment and not tied to any movable object.
void dGeomPlaneSetParams (dGeomID plane, dReal a, dReal b, dReal c, dReal d);
Set the parameters of the given plane.
void dGeomPlaneGetParams (dGeomID plane, dVector4 result);
Return in result the parameters of the given plane.
dReal dGeomPlanePointDepth (dGeomID plane, dReal x, dReal y, dReal z);
Return the depth of the point (x,y,z) in the given plane. Points inside the geom will have positive depth, points outside it will have negative depth, and points on the surface will have zero depth.
Note that planes in ODE are in fact not really planes: they are half-spaces. Anything that is moving inside the half-space will be ejected out from it. This means that planes are only planes from the perspective of one side. If you want your planes to be reversed, multiply the whole plane equation by -1.
Capsule Class
N.B. Capsule were called Capped Cylinder (CCylinder) before version 0.6
dGeomID dCreateCapsule (dSpaceID space, dReal radius, dReal length);
Create a capsule geom of the given parameters, and return its ID. If space is nonzero, insert it into that space.
A capsule is like a normal cylinder except it has half-sphere caps at its ends. This feature makes the internal collision detection code particularly fast and accurate. The cylinder's length, not counting the caps, is given by length. The cylinder is aligned along the geom's local Z axis. The radius of the caps, and of the cylinder itself, is given by radius.
void dGeomCapsuleSetParams (dGeomID capsule, dReal radius, dReal length);
Set the parameters of the given capsule.
void dGeomCapsuleGetParams (dGeomID capsule, dReal *radius, dReal *length);
Return in radius and length the parameters of the given capsule.
dReal dGeomCapsulePointDepth (dGeomID capsule, dReal x, dReal y, dReal z);
Return the depth of the point (x,y,z) in the given capsule. Points inside the geom will have positive depth, points outside it will have negative depth, and points on the surface will have zero depth.
Cylinder Class
dGeomID dCreateCylinder (dSpaceID space, dReal radius, dReal length);
Create a cylinder geom of the given parameters, and return its ID. If space is nonzero, insert it into that space.
void dGeomCylinderSetParams (dGeomID cylinder, dReal radius, dReal length);
Set the parameters of the given cylinder.
void dGeomCylinderGetParams (dGeomID cylinder, dReal *radius, dReal *length);
Return in radius and length the parameters of the given cylinder.
Ray Class
A ray is different from all the other geom classes in that it does not represent a solid object. It is an infinitely thin line that starts from the geom's position and extends in the direction of the geom's local Z-axis.
Calling dCollide between a ray and another geom will result in at most one contact point. Rays have their own conventions for the contact information in the dContactGeom structure (thus it is not useful to create contact joints from this information):
pos- This is the point at which the ray intersects the surface of the other geom, regardless of whether the ray starts from inside or outside the geom.
normal- This is the surface normal of the other geom at the contact point. if dCollide is passed the ray as its first geom then the normal will be oriented correctly for ray reflection from that surface (otherwise it will have the opposite sign).
depth- This is the distance from the start of the ray to the contact point.
Rays are useful for things like visibility testing, determining the path of projectiles or light rays, and for object placement.
dGeomID dCreateRay (dSpaceID space, dReal length);
Create a ray geom of the given length, and return its ID. If space is nonzero, insert it into that space.
void dGeomRaySetLength (dGeomID ray, dReal length);
Set the length of the given ray.
dReal dGeomRayGetLength (dGeomID ray);
Get the length of the given ray.
void dGeomRaySet (dGeomID ray, dReal px, dReal py, dReal pz, dReal dx, dReal dy, dReal dz);
Set the starting position (px,py,pz) and direction (dx,dy,dz) of the given ray. The ray's rotation matrix will be adjusted so that the local Z-axis is aligned with the direction. Note that this does not adjust the ray's length.
void dGeomRayGet (dGeomID ray, dVector3 start, dVector3 dir);
Get the starting position (start) and direction (dir) of the ray. The returned direction will be a unit length vector.
void dGeomRaySetParams( dGeomID ray, int FirstContact, int BackfaceCull ); void dGeomRayGetParams( dGeomID ray, int *FirstContact, int *BackfaceCull ); void dGeomRaySetClosestHit( dGeomID ray, int ClosestHit ); int dGeomRayGetClosestHit( dGeomID ray );
Set or Get parameters for the ray which determine which hit between the ray geom and a trimesh geom is returned from dCollide.
FirstContact determines if dCollide returns the first collision detected between the ray geom and a trimesh geom, even if that collision is not the nearest to the ray start position. BackfaceCull determines if dCollide returns a collision between the ray geom and a trimesh geom when the collision is between the ray and a backfacing triangle. Default values are FirstContact = 0, BackfaceCull = 0 (both false).
ClosestHit determines if dCollide returns the closest hit between the ray and a trimesh geom. If ClosestHit is false, the hit returned by dCollide may not be the nearest collision to the ray position. This parameter is ignored if FirstContact is set to true in dGeomRaySetParams(). If ClosestHit is set to true and BackfaceCull is set to false, the hit returned by dCollide may be between the ray and a backfacing triangle. The default value is ClosestHit = 0 (false).
Convex Class
dGeomID dCreateConvex (dSpaceID space, dReal *planes, unsigned planecount,
dReal *points, unsigned pointcount, unsigned *polygons);
void dGeomSetConvex (dGeomID g, dReal *planes, unsigned planecount,
dReal *points, unsigned pointcount, unsigned *polygons);
Triangle Mesh Class
A triangle mesh (TriMesh) represents an arbitrary collection of triangles. The triangle mesh collision system has the following features:
- Any triangle "soup" can be represented --- i.e. the triangles are not required to have any particular strip, fan or grid structure.
- Triangle meshes can interact with spheres, boxes, rays and other triangle meshes.
- It works well for relatively large triangles.
- It uses temporal coherence to speed up collision tests. When a geom has its collision checked with a trimesh once, data is stored inside the trimesh. This data can be cleared with the dGeomTriMeshClearTCCache function. In the future it will be possible to disable this functionality.
Trimesh/Trimesh collisions, perform quite well, but there are three minor caveats:
- The stepsize you use will, in general, have to be reduced for accurate collision resolution. Non-convex shape collision is much more dependent on the collision geometry than primitive collisions. Further, the local contact geometry will change more rapidly (and in a more complex fashion) for non-convex polytopes than it does for simple, convex polytopes such as spheres and cubes.
- In order to efficiently resolve collisions, dCollideTTL needs the positions of the colliding trimeshes in the previous timestep. This is used to calculate an estimated velocity of each colliding triangle, which is used to find the direction of impact, contact normals, etc. This requires the user to update these variables at every timestep. This update is performed outside of ODE, so it is not included in ODE itself. The code to do this looks something like this:
const double *DoubleArrayPtr = Bodies(BodyIndex).TransformationMatrix->GetArray(); dGeomTriMeshDataSet( TriMeshData, TRIMESH_LAST_TRANSFORMATION, (void *) DoubleArrayPtr );
The transformation matrix is the standard 4x4 homogeneous transform matrix, and the "DoubleArray" is the standard flattened array of the 16 matrix values.
NOTE: The triangle mesh class is not final, so in the future API changes might be expected.
NOTE: dInitODE() must have been called in order to successfully use Trimesh.
dTriMeshDataID dGeomTriMeshDataCreate(); void dGeomTriMeshDataDestroy (dTriMeshDataID g);
Creates and destroys a dTriMeshData object which is used to store mesh data.
void dGeomTriMeshDataBuild (dTriMeshDataID g,
const void* Vertices, int VertexStride, int VertexCount,
const void* Indices, int IndexCount, int TriStride,
const void* Normals);
NOTE: The argument order is non-intuitive here: stride,count for vertex data, but count,stride for index data.
Used for filling a dTriMeshData object with data. No data is copied here, so the pointers passed into this function must remain valid. This is how the strided data works:
struct StridedVertex {
dVector3 Vertex; // 4th component can be left out, reducing memory usage
// Userdata
};
int VertexStride = sizeof (StridedVertex);
struct StridedTri {
int Indices(3);
// Userdata
};
int TriStride = sizeof (StridedTri);
The Normals argument is optional: the normals of the faces of each trimesh object. For example,
dTriMeshDataID TriMeshData;
TriMeshData = dGeomTriMeshGetTriMeshDataID ( Bodies(BodyIndex).GeomID); // as long as dReal == floats
dGeomTriMeshDataBuildSingle (TriMeshData,
Bodies(BodyIndex).VertexPositions, 3*sizeof(dReal), (int) numVertices, // Vertices
Bodies(BodyIndex).TriangleIndices, 3*((int) NumTriangles), 3*sizeof(unsigned int), // Faces
Bodies(BodyIndex).FaceNormals); // Normals
This pre-calculation saves some time during evaluation of the contacts, but isn't necessary. If you don't want to calculate the face normals before construction (or if you have enormous trimeshes and know that only very few faces will be touching and want to save time), just pass a "NULL" for the Normals argument, and dCollideTTL will take care of the normal calculations itself.
void dGeomTriMeshDataBuildSimple (dTriMeshDataID g,
const dVector3*Vertices, int VertexCount,
const int* Indices, int IndexCount);
Simple build function provided for convenience.
typedef int dTriCallback (dGeomID TriMesh, dGeomID RefObject, int TriangleIndex); void dGeomTriMeshSetCallback (dGeomID g, dTriCallback *Callback); dTriCallback* dGeomTriMeshGetCallback (dGeomID g);
Optional per triangle callback. Allows the user to say if collision with a particular triangle is wanted. If the return value is zero no contact will be generated.
typedef void dTriArrayCallback (dGeomID TriMesh, dGeomID RefObject, const int* TriIndices, int TriCount); void dGeomTriMeshSetArrayCallback (dGeomID g, dTriArrayCallback* ArrayCallback); dTriArrayCallback *dGeomTriMeshGetArrayCallback (dGeomID g);
Optional per geom callback. Allows the user to get the list of all intersecting triangles in one shot.
typedef int dTriRayCallback (dGeomID TriMesh, dGeomID Ray, int TriangleIndex, dReal u, dReal v); void dGeomTriMeshSetRayCallback (dGeomID g, dTriRayCallback* Callback); dTriRayCallback *dGeomTriMeshGetRayCallback (dGeomID g);
Optional Ray callback. Allows the user to determine if a ray collides with a triangle based on the barycentric coordinates of an intersection. The user can for example sample a bitmap to determine if a collision should occur.
dGeomID dCreateTriMesh (dSpaceID space, dTriMeshDataID Data,
dTriCallback *Callback,
dTriArrayCallback *ArrayCallback,
dTriRayCallback *RayCallback);
Constructor. The Data member defines the vertex data the newly created triangle mesh will use.
void dGeomTriMeshSetData (dGeomID g, dTriMeshDataID Data);
Replaces the current data.
void dGeomTriMeshClearTCCache (dGeomID g);
Clears the internal temporal coherence caches.
void dGeomTriMeshGetTriangle (dGeomID g, int Index, dVector3 *v0, dVector3 *v1, dVector3 *v2);
Retrieves a triangle in world space. The v0, v1 and v2 arguments are optional.
void dGeomTriMeshGetPoint (dGeomID g, int Index, dReal u, dReal v, dVector3 Out);
Retrieves a position in world space based on the incoming data.
void dGeomTriMeshEnableTC(dGeomID g, int geomClass, int enable); int dGeomTriMeshIsTCEnabled(dGeomID g, int geomClass);
These functions can be used to enable/disable the use of temporal coherence during tri-mesh collision checks. Temporal coherence can be enabled/disabled per tri-mesh instance/geom class pair, currently it works for spheres and boxes. The default for spheres and boxes is 'false'.
The 'enable' param should be 1 for true, 0 for false.
Temporal coherence is optional because allowing it can cause subtle efficiency problems in situations where a tri-mesh may collide with many different geoms during its lifespan. If you enable temporal coherence on a tri-mesh then these problems can be eased by intermittently calling dGeomTriMeshClearTCCache for it.
typedef int dTriTriMergeCallback(dGeomID TriMesh, int FirstTriangleIndex, int SecondTriangleIndex); void dGeomTriMeshSetTriMergeCallback(dGeomID g, dTriTriMergeCallback* Callback); dTriTriMergeCallback* dGeomTriMeshGetTriMergeCallback(dGeomID g);
Allows the user to generate a fake triangle index for a new contact generated from merging of two other contacts. That index could later be used by the user to determine attributes of original triangles used as sources for a merged contact. The callback is currently used within OPCODE trimesh-sphere and OPCODE new trimesh-trimesh collisions.
If the callback is not assigned (the default) -1 is generated as triangle index for merged contacts.
NOTE: Before this API was introduced, the index was always set to the first triangle index.
Heightfield Class
dHeightfield is a regular grid heightfield collider. It can be used for heightmap terrains, but also for deformable animated water surfaces.
Heightfield Data
The dHeightfieldData is a storage class, similar to the dTrimeshData class, that holds all geom properties and optionally height sample data.
dHeightfieldDataID dGeomHeightfieldDataCreate (); void dGeomHeightfieldDataDestroy (dHeightfieldDataID d)
Allocate and destroy dHeightfieldDataID objects. You must call dGeomHeightfieldDataDestroy to destroy it after the geom has been removed. The dHeightfieldDataID value is used when specifying a data format type.
Building from existing data
There are four functions to easily build a heightfield from an array of height values of different data types. They all have the same parameters, except the data type of the pHeightData pointer is different:
void dGeomHeightfieldDataBuildByte (dHeightfieldDataID d,
const unsigned char *pHeightData,
int bCopyHeightData,
dReal width, dReal depth,
int widthSamples, int depthSamples,
dReal scale, dReal offset, dReal thickness, int bWrap);
void dGeomHeightfieldDataBuildShort (dHeightfieldDataID d,
const short *pHeightData,
int bCopyHeightData,
dReal width, dReal depth,
int widthSamples, int depthSamples,
dReal scale, dReal offset, dReal thickness, int bWrap);
void dGeomHeightfieldDataBuildSingle (dHeightfieldDataID d,
const float *pHeightData,
int bCopyHeightData,
dReal width, dReal depth,
int widthSamples, int depthSamples,
dReal scale, dReal offset, dReal thickness, int bWrap);
void dGeomHeightfieldDataBuildDouble (dHeightfieldDataID d,
const double *pHeightData,
int bCopyHeightData,
dReal width, dReal depth,
int widthSamples, int depthSamples,
dReal scale, dReal offset, dReal thickness, int bWrap);
Loads heightfield sample data into the HeightfieldData structure. Before a dHeightfieldDataID can be used by a geom it must be configured to specify the format of the height data. These calls all take the same parameters as listed below; the only difference is the data type pointed to by pHeightData.
pHeightDatais a pointer to the height data;bCopyHeightDataspecifies whether the height data should be copied to a local store. If zero, the data is accessed by reference and so must persist throughout the lifetime of the heightfield;width,heightare the world space heightfield dimensions on the geom's local X and Z axes;widthSamples,depthSamplesspecifies the number of vertices to sample along the width and depth of the heightfield. Naturally this value must be at least two or more;scaleis the vertical sample height multiplier, a uniform scale applied to all raw height data;offsetis the vertical sample offset, added to the scaled height data;thicknessis the thickness of AABB which is added below the lowest point, to prevent objects from falling through very thin heightfields;bWrapis 0 if the heightfield should be finite, 1 if should tile infinitely.
Retrieving data from a callback
typedef dReal (*dHeightfieldGetHeight) (void *userdata, int x, int z);
void dGeomHeightfieldDataBuildCallback (dHeightfieldDataID d,
void *pUserData,
dHeightfieldGetHeight *pCallback,
dReal width, dReal depth,
int widthSamples, int depthSamples,
dReal scale, dReal offset, dReal thickness, int bWrap);
This call specifies that the heightfield data is computed by the user and it should use the given callback when determining the height of a given element of its shape. The callback function is called while the simulation runs, and returns the value of the heightmap ("y" value) at a given (x,z) position.
pUserDatais a pointer for arbitrary user-defined data to pass to the callbackpCallbackis a pointer to the callback function- The other arguments are the same as the other dGeomHeightfieldDataBuild* functions.
Setting terrain bounds
void dGeomHeightfieldDataSetBounds (dHeightfieldDataID d, dReal min_height, dReal max_height)
Sets the minimum and maximum height sample bounds in sample space. ODE does not automatically detect the sample data minimum and maximum height bounds, this must be done manually (for added flexibility and allows the user to control the process).
The default vertical sample bounds are infinite, so when the sample bounds are known, call this function for improved performance. Also, if the geom (built from this data) is rotated, its AABB will end up with NaNs, and break the collision detection; so always set the heightfield data's bounds to finite values if you are going to rotate the geom.
Heightfield Geom
dGeomID dCreateHeightfield(dSpaceID space, dHeightfieldDataID data, int bPlaceable);
Uses the information in the given dHeightfieldDataID to construct a geom representing a heightfield in a collision space.
dHeightfieldDataIDis the heightfield data objectbPlaceabledefines whether this geom can be transformed in the world using the usual functions such as dGeomSetPosition and dGeomSetRotation. If the geom is not set as placeable, then it uses a fixed orientation where the global Y axis represents the 'height' of the heightfield.
void dGeomHeightfieldSetHeightfieldData(dGeomID g, dHeightfieldDataID Data); dHeightfieldDataID dGeomHeightfieldGetHeightfieldData(dGeomID g);
Set and retrieve the heightfield data object of this geom.
Geometry Transform Class
The geom transform classes are deprecated. Use geom offsets instead.
dGeomID dCreateGeomTransform (dSpaceID space); void dGeomTransformSetGeom (dGeomID g, dGeomID obj); dGeomID dGeomTransformGetGeom (dGeomID g); void dGeomTransformSetCleanup (dGeomID g, int mode); int dGeomTransformGetCleanup (dGeomID g); void dGeomTransformSetInfo (dGeomID g, int mode); int dGeomTransformGetInfo (dGeomID g);
If your code uses geom transforms, update it to use geom offsets instead, as soon as possible. The geom transform functions will be removed from the next release.
User defined classes
ODE's geometry classes are implemented internally as C++ classes. If you want to define your own geometry classes you can do this in two ways:
- Use the C functions in this section. This has the advantage of providing a clean separation between your code and ODE.
- Add the classes directly to ODE's source code. This has the advantage that you can use C++ so the implementation will potentially be a bit cleaner. This is also the preferred method if your collision class is generally useful and you want to contribute it to the public source base.
What follows is the C API for user defined geometry classes.
Every user defined geometry class has a unique integer number. A new geometry class (call it 'X') must provide the following to ODE:
- Functions that will handle collision detection and contact generation between X and one or more other classes. These functions must be of type
dColliderFn, which is defined as:
typedef int dColliderFn (dGeomID o1, dGeomID o2, int flags, dContactGeom *contact, int skip);
This has exactly the same interface as dCollide. Each function will handle a specific collision case, where o1 has type X and o2 has some other known type.
- A "selector" function, of type
dGetColliderFnFn, which is defined as:
typedef dColliderFn * dGetColliderFnFn (int num);
This function takes a class number (num), and returns the collider function that can handle colliding X with class num. It should return 0 if X does not know how to collide with class num. Note that if classes X and Y are to collide, only one needs to provide a function to collide with the other.
This function is called infrequently - the return values are cached and reused.
- A function that will compute the axis aligned bounding box (AABB) of instances of this class. This function must be of type
dGetAABBFn, which is defined as:
typedef void dGetAABBFn (dGeomID g, dReal aabb[6]);
This function is given g, which has type X, and returns the axis-aligned bounding box for g. The aabb array has elements (minx, maxx, miny, maxy, minz, maxz). If you don't want to compute tight bounds for the AABB, you can just supply a pointer to dInfiniteAABB, which returns +/- infinity in each direction.
- The number of bytes of "class data" that instances of this class need. For example a sphere stores its radius in the class data area, and a box stores its side lengths there.
The following things are optional for a geometry class:
- A function that will destroy the class data. Most classes will not need this function, but some will want to deallocate heap memory or release other resources. This function must be of type
dGeomDtorFn, which is defined as:
typedef void dGeomDtorFn (dGeomID o);
The argument o has type X.
- A function that will test whether a given AABB intersects with an instance of X. This is used as an early-exit test in the space collision functions. This function must be of type
dAABBTestFn, which is defined as:
typedef int dAABBTestFn (dGeomID o1, dGeomID o2, dReal aabb2[6]);
The argument o1 has type X. If this function is provided it is called by dSpaceCollide when o1 intersects geom o2, which has an AABB given by aabb2. It returns 1 if aabb2 intersects o1, or 0 if it does not.
This is useful, for example, for large terrains. Terrains typically have very large AABBs, which are not very useful to test intersections with other objects. This function can test another object's AABB against the terrain without going to the computational trouble of calling the specific collision function. This has an especially big savings when testing against GeomGroup objects.
Here are the functions used to manage custom classes:
int dCreateGeomClass (const dGeomClass *classptr);
Register a new geometry class, defined by classptr. The number of the new class is returned. The convention used in ODE is to assign the class number to a global variable with the name dXxxClass where Xxx is the class name (e.g. dSphereClass).
Here is the definition of the dGeomClass structure:
struct dGeomClass {
int bytes; // bytes of custom data needed
dGetColliderFnFn *collider; // collider function
dGetAABBFn *aabb; // bounding box function
dAABBTestFn *aabb_test; // aabb tester, can be 0 for none
dGeomDtorFn *dtor; // destructor, can be 0 for none
};
void * dGeomGetClassData (dGeomID);
Given a geom, return a pointer to the class's custom data (this will be a block of the required number of bytes).
dGeomID dCreateGeom (int classnum);
Create a geom of the given class number. The custom data block will initially be set to 0. This object can be added to a space using dSpaceAdd.
When you implement a new class you will usually write a function that does the following:
- If the class has not yet been created, create it. You should be careful to only ever create the class once.
- Call dCreateGeom to make an instance of the class.
- Set up the custom data area.
Composite objects
Consider the following objects:
- A table that is made out of a box for the top and a box for each leg.
- A branch of a tree that is modeled from several cylinders joined together.
- A molecule that has spheres representing each atom.
If these objects are meant to be rigid then it is necessary to use a single rigid body to represent each of them. But it might seem that performing collision detection is a problem, because there is no single geometry class that can represent a complex shape like a table or a molecule. The solution is to use a composite collision object that is a combination of several geoms.
No extra functions are needed to manage composite objects: simply create each component geom and attach it to the same body. To move and rotate the separate geoms with respect to each other in the same object, geometry offsets can be used. That's all there is to it!
However there is one caveat: You should never create a composite object that will result in collision points being generated very close together. For example, consider a table that is made up of a box for the top and four boxes for the legs. If the legs are flush with the top, and the table is lying on the ground on its side, then the contact points generated for the boxes may coincide where the legs join to the top. ODE does not currently optimize away coincident contact points, so this situation can lead to numerical errors and strange behavior.
In this example the table geometry should be adjusted so that the legs are not flush with the sides, making it much more unlikely that coincident contact points will be generated. In general, avoid having different contact surfaces that overlap, or that line up along their edges.
Utility functions
void dClosestLineSegmentPoints (const dVector3 a1, const dVector3 a2,
const dVector3 b1, const dVector3 b2,
dVector3 cp1, dVector3 cp2);
Given two line segments A and B with endpoints a1-a2 and b1-b2, return the points on A and B that are closest to each other (in cp1 and cp2). In the case of parallel lines where there are multiple solutions, a solution involving the endpoint of at least one line will be returned. This will work correctly for zero length lines, e.g. if a1==a2 and/or b1==b2.
int dBoxTouchesBox (const dVector3 p1, const dMatrix3 R1, const dVector3 side1,
const dVector3 p2, const dMatrix3 R2, const dVector3 side2);
Given boxes (p1,R1,side1) and (p2,R2,side2), return 1 if they intersect or 0 if not. p is the center of the box, R is the rotation matrix for the box, and side is a vector of x/y/z side lengths.
void dInfiniteAABB (dGeomID geom, dReal aabb[6]);
This function can be used as the AABB-getting function in a geometry class, if you don't want to compute tight bounds for the AABB. It returns +/- infinity in each direction.
Implementation notes
Large Environments
Often the collision world will contain many objects that are part of the static environment, that are not associated with rigid bodies. ODE's collision detection is optimized to detect geoms that do not move and to precompute as much information as possible about these objects to save time. For example, bounding boxes and internal collision data structures are precomputed.
Using a Different Collision Library
Using ODE's collision detection is optional - an alternative collision library can be used as long as it can supply dContactGeom structures to initialize contact joints.
The dynamics core of ODE is mostly independent of the collision library that is used, except for four points:
- The
dGeomIDtype must be defined, as each body can store a pointer to the first geometry object that it is associated with.
- The
dGeomMoved()function must be defined, with the following prototype:
void dGeomMoved (dGeomID);
This function is called by the dynamics code whenever a body moves: it indicates that the geometry object associated with the body is now in a new position.
- The
dGeomGetBodyNext()function must be defined, with the following prototype:
dGeomID dGeomGetBodyNext (dGeomID);
This function is called by the dynamics code to traverse the list of geoms that are associated with each body. Given a geom attached to a body, it returns the next geom attached to that body, or 0 if there are no more geoms.
- The
dGeomSetBody()function must be defined, with the following prototype:
void dGeomSetBody (dGeomID, dBodyID);
This function is called in the body destructor code (with the second argument set to 0) to remove all references from the geom to the body.
If you want an alternative collision library to get body-movement notifications from ODE, you should define these types and functions appropriately.
How To Make Good Simulations
How To Make Good Simulations
(just notes for now)
Integrator accuracy and stability
- integrator will not give exact solution
- what is stabilty
- integrator types (exp & imp, order)
- tradeoff between accuracy, stability and work
Behavior may depend on step size
- smaller step = more accurate, more stable
- 10*0.1 not the same as 5*0.2
- tweak at final frame rate
Making things go faster
What factors does execution speed depend on? Each joint removes a number of degrees of freedom (DOFs) from the system. For example the ball and socket removes three, and the hinge removes five. For each separate group of bodies connected by joints, where:
- m1 is the number of joints in the group,
- m2 is the total number of DOFs removed by those joints, and
- n is the number of bodies in the group, then the computing time per step for the group is proportional to: k1 O(m1) + k2 O(m23) + k2 O(n)
ODE currently relies on factorization of a "system" matrix that has one row/column for each DOF removed (this is where the O(m23) comes from). In a 10 body chain that uses ball and socket joints, roughly 30-40% of the time is spent filling in this matrix, and 30-40% of the time is spent factorizing it.
Thus, to speed up your simulation you might consider:
- Using less joints - often small bodies and their associated joints can be replaced by purely kinematic "fakes" without harming physical realism.
- Replacing multiple joints with simpler alternatives. This will become easier as more specialized joint types are defined.
- Using less contacts.
- Preferring frictionless or viscous friction contacts (that remove one DOF) over Coulomb friction contacts (that remove three DOFs) where possible. In the future ODE will implement techniques that scale better with the number of joints.
Making things stable
- stiff springs / stiff forces are bad.
- hard constraints are good.
- dependence on integration timestep.
- Use powered joint, joint limits, built-in springs as much as possible, avoid explicit forces.
- if bodies move faster than is reasonable for the timestep
- inertias with long axes
- mass ratios - e.g. a whip. Joints that connect large and small masses together will have a harder time keeping their error low.
- object size ratios. If a sphere of size 1 has to roll over a polygon a 1000 units long, you might start to see the ball jitter slightly, or in some cases even start to suddenly bounce while it was lying still on the ground. This can easily be solved by subdividing the polygon into several smaller polygons.
- Increasing the global CFM will make the system more numerically robust and less susceptible to stability problems. It will also make the system look more "spongy", so a tradeoff has to be found.
- Redundant constraints (two or more constraints that "try and do the same job") will fight each other and cause stability problems. The numerical cause of this problem is singularity in the system matrix. One example of this is if two contacts joints connect the same pair of bodies at the same point. Another example is if a virtual hinge joint is created between two bodies by connecting them with two ball joints, spaced apart along the hinge axis (this is bad because the two ball joints try to remove six degrees of freedom from the system, but a real hinge joint would only remove five). Redundant constraints fight each other and generate strange forces in the system that can swamp the normal forces. For example, an affected body might fly around as though it has a life of its own, with complete disregard for gravity.
Using constraint force mixing (CFM)
- allow singular configurations
- effects: jitter or strange forces due to error amplification, LCP solver may go slow
- allow compliant joints (this may be unwanted also)
Avoiding singularities
- Singularity occurs when there are more joints than needed to constrain the bodies motions.
- Multiple (incompatible) joints between bodies, esp joint + contact (don't collide objects that are joined together).
- increasing CFM
- unintentional - box chain on floor, other assemblies
- use minimum joints for correct behavior. use correct joints for desired behavior
- adding global CFM usually helps
Other stuff
- contact jitter when pushed out too far - soln: use softness
- keep lengths and masses around 1
- LCP solver takes a variable number of iterations (only non-deterministic part). if it takes too long, increase global CFM, prevent multiple contacts (or similar), and limit high ratio of force magnitudes (tree grabbing problem)
- hinge limits outside +/- pi
FAQ
Add questions and answers here. Longer answers should preferably be broken off into their own pages and referenced via a Wiki Link. The ODE mailing list has hosted an active discussion of ODE since late 2001. Many topics not covered on this page have been discussed on the mailing list. Click here to search the mailing list with Google.
Compiling ODE
Where can I get a precompiled library for Visual Studio?
I don't want to/can't get the makefile working with Microsoft Visual C++. How do I compile ODE?
Basically, you create a project, tweak some of the options for the config.h header, add all the cpp files in ode/src/ (except for a few that cause problems) into the project, include the drawstuff files, add all necessary include directories, add opengl32.lib and glu32.lib to the link line, and compile. Detailed instructions can be found in the Building ODE with MSVC6 section.
I've compiled the ODE test programs with Microsoft Visual C++, but when I try to run them I get the error message "could not load accelerators." What am I doing wrong?
Add the resource files "ode/drawstuff/src/resources.rc" and "ode/drawstuff/src/resource.h" to your project.
I get an error during linking, "unresolved external symbol."
Basically, you need to learn how to include more than one source file in your project. This is a very basic thing in programming, the manual will tell you how to do it, as will almost any book on programming that describes your compiler. The short version is, do a "find in files" or grep for the symbol that's unresolved to find out which source file its defined in. Don't include any leading underscores in your search. Then, make sure that file is included in your project. It can be included in one of two ways: either directly, the way you include the source files you've written, or as part of a "dynamic linked library" or "shared library." If you're using Microsoft Visual C++ on windows and you're new to programming, you'll probably have more luck if you ditch the makefile and use the MSVC project.
Is there a working solution for MSVC7?
There are two methods for building ODE using MSVC7 (.NET) - you can use the project files provided in the contrib/msvc7 directory of the ODE distribution, or you can check out the Building ODE with VS.NET recipe that takes a command line approach, which fits more naturally with the expected ODE build process. If you take the project file approach, you may find that you need to do a fair amount of tweaking since it may be out of date with the current ODE code structure. Note that you must have OPCODE installed to build the tri-collider version of the MSVC7 project files. COMMENT: I built ODE today on VS.NET followin the instructions Building ODE with MSVC6, it worked okay. I couldn't build all the samples, but that's only a couple of errors with stdlib etc. I think. I later tried the project files in contrib/msvc7, but they didn't work, I got lots of linker errors.
In MSVC7 i get the error "error LNK2019: unresolved external symbol __ftol2".
Try adding this to the top of ode.ccp:
#if (_MSC_VER >= 1300) && (WINVER < 0x0500)
//VC7 or later, building with pre-VC7 runtime libraries
extern "C" long _ftol( double ); //defined by VC6 C libs
extern "C" long _ftol2( double dblSource ) { return _ftol( dblSource ); }
#endif
Using ODE
I found a bug, how do I get it fixed?
Please report bugs using the SourceForge Bug Tracker. You can also request new features.
I reported a bug/requested a feature and no one has done anything about it. Why not?
Unlike some open-source projects, ODE does not have a core group of regular developers. Additions and improvements depend entirely on contributions from the community. While there have been some problems with this approach in the past, the situation is steadily improving. If you would like to join the cause, start by getting the latest source code and then submit a patch.
What units should I use with ODE?
- Short Answer: Metric, MKS (Metre-Kilogram-Second), thus your lengths will be expressed in meters, masses in kilograms, and timestep in seconds.
- Slightly Longer Answer: "SI Units" or "The international system of Units", http://physics.nist.gov/cuu/Units/ SI units is the technical term for Meter-Kilogram-Second. By always using SI units in calculations, you'll always get SI units out at the other end; you won't end up with nasty multipliers.
- Longer Answer: technically, ODE doesn't use specific units. You can use anything you wish, as long as you stay consistent with yourself. For example, you could scale all your values by Pi, and everything will be fine. Being consistent with yourself is what SI units *is*; remember though that you multiply everything by pi, then your acceleration will include a pi^2 factor. This only gets uglier as it goes... stick with meters-kilograms-seconds
- Longer, Slightly Sillier, Imperial, Answer: Furlongs per fortnight per hour is a perfectly accurate and meaningful description of linear acceleration, but trying to work out how far you've travelled in three minutes at that acceleration starting at zero gives you a lot of ugly multipliers.
How can I make my actor capsule (capped cylinder) stay upright?
Manually reset the orientation with each frame, use an angular motor, apply torques, use a sphere instead, or (quoting Jon Watte) instead use "a hovering sphere with a ray to 'sense' where the ground is and apply spring forces to keep it at a constant height above ground." See 1, 2, 3 for details.
A HOWTO is being set-up over here: HOWTO upright capsule
How do I simulate a wheeled-vehicle?
Check the HOWTO build a 4 wheel vehicle article.
How do I stop my car from flipping over?
Jon Watte has create an excellent demo called CarWorld. It is a bit dated and will probably not compile against the latest versions of ODE, but should tell you everything you need to know about creating convincing wheeled vehicles in ODE. He also made a more recent and leaner demo called RayCar.
A HOWTO is being set-up here: HOWTO build a 4 wheel vehicle
Can ODE be used in PS2, Gamecube or XBox games?
Can I use ODE in language X?
ODE bindings exist for many programming languages. See ODE in other languages for details.
Can I save and restore an ODE simulation? Will the resumed simulations always continue identically?
Yes, and yes, but there are many things to take into consideration. See HOWTO save and restore
How do I create an object with mass distributed non-uniformly?
An object with a non-uniform mass acts as though the mass were all accumulated at the center of gravity - except that the rotational inertia tensor is noticably different. I recommend reading the O'Reilly book "Physics for Game Developers" which explains clearly how to compute that tensor.
How do I stop things from rolling off into infinity, or pendulums from swinging forever?
ODE models a universe with frictionless hinges and no rolling friction, so problems like those are fairly common.
See the Damping HOWTO.
My simulation jitters and/or explodes. How do I get a stable simulation?
Please see the HOWTO make the simulation better
How can I implement my collision callback as a C++ member function?
See Collision callback member function.
How can I simulate a servo motor?
dReal Gain = 0.1; dReal MaxForce = 100; dReal TruePosition = dJointGetHingeAngle(joint); dReal DesiredPosition = /* whatever */; dReal Error = TruePosition - DesiredPosition; dReal DesiredVelocity = -Error * Gain; dJointSetHingeParam(joint[a], dParamFMax, MaxForce); dJointSetHingeParam(joint[a], dParamVel, DesiredVelocity);
The Gain and MaxForce parameters can be tuned to get the desired stiffness and strength from the joint.
My wheels are sloppy; they don't stay straight when I turn them.
Assuming that you have already enabled finite rotation mode, and set the correct axis each step, you may be bitten by a problem in the joint angle constraints. If you try to set a stop that's inconsistent (hi < lo, etc), then the setter will silently ignore the data. Thus, if hi and low are set to 0.1, and you want to set them to 0.0, the first call to set hi to 0.0 will fail (beacause lo is 0.1); the call to set lo will succeed, leaving the stops at [0.0,0.1]. The solution is to set the hi, then set the lo, then set the hi again -- this will always work, no matter which direction you're trying to move the stops. Getting a vehicle to behave correctly, including wheel behaviour at high speed, isn't as trivial as expected. Look around for working examples, like Jon Watte's CarWorld and the leaner RayCar. See HOWTO build a 4 wheel vehicle
How do I come up with the optimum values for the parameters to dHashSpaceSetLevels?
They just really depend on the typical sizes of collidable geom (groups) in your space. Set minlevel and maxlevel such that your full range of geom sizes are encompassed. Say that your largest geoms are of size 41 units (in X or Y or Z dimension) and your smallest are 0.25 units in size. Then your dHashSpaceSetLevels? call should be: dHashSpaceSetLevels?(space, -2, 6) to set the min and max cell sizes to 2^-2 = 0.25 and 2^6=64 (2^6 being the smallest power of 2 that '41' will fit in). It's more important to get the max right than to get the min right, assuming that your tiniest objects don't all clump together in the bottom of a hole. You can be over-generous with these values and just suffer a smidgen of time+space overhead. But if you're too stingy, your collision times start to look decreasingly like O(n) and more like O(n^2).
How do I make my AI apply the correct amount of force to move to a particular position?
Please see the HOWTO thrust control logic page.
I have a model loaded from an obj. How can i associate it with a body?
Create a new body (dBodyCreate) for your object. Then use that body's matrix (see "ODE and Graphics" below) as your model/world matrix when you render. How you do that is entirely dependent on your application or engine.
What is the best way to apply physics to a controllable avatar on a landscape?
This has been discussed several times in the mailing list; can someone post some links?
My trimesh object is falling through the floor!
Trimesh-Plane collision wasn't implemented until after the 0.6 release. You can get it from the Subversion repository while you wait for the next release.
My trimesh object doesn't collide at all!
Try inverting the normals. (FIXME: give more detail)
If you have a wavefront obj file for example. (vertices are defined as v [x y z], and faces as f [v1 v2 v3])
To invert the face normals you have to reorder the vertices of the face:
original face: f 1 2 3 4 inverted face: f 1 4 3 2
GLMmodel::glmReverseWinding() can do this for you.
I'm using variable timesteps, and getting odd behaviour!
ODE is made to work with fixed timesteps. It's possible to get it to work with variable timesteps, but not trivial. (No, this editor doesn't know how to)
Why not? For example, think of an object "resting" on the ground. It'll actually stabilize at a small depth into the ground. When step sizes vary, the ideal stable position will change at each step, and thus the object will jitter (and may very well gain energy!)
FIXME: It'd be really nice if someone who implemented it could fill out a HOWTO fixed vs variable timestep
I get "ODE Message 3: LCP internal error, s <= 0 (s=0.0000e+00)"
It happens. It is usually caused by an object ramming into another with too much force (or just the right force). Try decreasing the mass of the object, or changing the timestep. Nevertheless, this won't crash your simulation, so you could ignore it as a warning.
LCP stands for linear complementarity problem (see: [1]), a linear algebra problem of finding two vectors that satisfies a certain set of equations based on a square matrix and a column vector. This problem is quite common in optimization, physics simulation and mathematical programming. ODE uses a method developed by (Cottle & Dantzig 1968) .
My (stacks of) boxes are unstable!
Make sure that you are using a constant timestep. Using a variable timestep will result in varying errors in the solver, causing instability.
Make sure that you are generating enough contacts. Most objects need at least three contacts to be stable - this applies to real-world physics too.
Add a small damping force and torque to each box in each frame. You can do this by taking the velocity (linear or angular) of the box, multiplying by a negative coefficient (-0.02 for example) and adding the result back as force (or torque).
Turn on auto-disable. You may need to increase the threshold slightly.
ODE and Graphics
How do I run the simulation without the graphics or with my own graphics code?
The ODE library itself only provides simulation, not graphics code. The example programs have their own very simple graphics code written in OpenGL. To make the example programs simpler, the common graphics code has been split into a very simple graphics library called DrawStuff?. To run ODE without graphics, you want to call dWorldStep?() in a loop. So, read the documentation and look at the example code.
Can I use ODE with DirectX?
Yes, in fact a couple of people already have. Some people say that ODE has one handedness and DirectX another, but that's a myth. ODE doesn't assume any handedness, its only when you hook it up to inputs and outputs that handedness becomes an issue. Microsoft uses left-handed clockwise-winding conventions, which has been used traditionally in computer graphics for a long time (POV-ray is left handed, for example); OpenGL uses right-handed counter-clockwise-winding convetions, which have been used in mathematics and physics for hundreds of years. Which goes to show that the good thing about standards is that there are so many to choose from!
Anyway, here are some ways to convert from ODE to DirectX. As you see, it's very simple -- if you plug in consistent numbers in one coordinate system, and apply all the conventions of that coordinate system, then the numbers you get out are, still, in that coordinate system. The only thing you may need to worry about is triangle winding order; if your mesh uses a winding order that's different from the default for the coordinate system you're using, you need to invert the winding of your triangles.
D3DXVECTOR3 convertVector(const dReal *in)
{
D3DXVECTOR3 out;
out.x=(float) in[0];
out.y=(float) in[1];
out.z=(float) in[2];
return out;
}
D3DXQUATERNION convertQuaternion(const dReal *in)
{
D3DXQUATERNION out;
out.x=(float)in[1];
out.y=(float)in[2];
out.z=(float)in[3];
out.w=(float)in[0];
return out;
}
// Second argument can be the value returned by dBodyGetRotation(bodyID)
void convertMatrix(D3DXMATRIX &t, const dReal *bMat)
{
t._11 = bMat[0];
t._12 = bMat[1];
t._13 = bMat[2];
t._14 = 0;
t._21 = bMat[4];
t._22 = bMat[5];
t._23 = bMat[6];
t._24 = 0;
t._31 = bMat[8];
t._32 = bMat[9];
t._33 = bMat[10];
t._34 = 0;
}
- I have been using different matrix conversion code. Somewhere last month I started using above, and somehow the rotations are mirrored. After Lots of testing I found the problem, it was my alterated matrix function (the above one). I got my old one back from a backup, and everything rotated like it should. Here is my version:
void convertMatrix(D3DXMATRIX &t, const dReal *bMat)
{
t._11 = bMat[0];
t._12 = bMat[4];
t._13 = bMat[8];
t._14 = 0;
t._21 = bMat[1];
t._22 = bMat[5];
t._23 = bMat[9];
t._24 = 0;
t._31 = bMat[2];
t._32 = bMat[6];
t._33 = bMat[10];
t._34 = 0;
}
I hope this might help someone.
From D3DXMATRIX to an ODE matrix
I had quite some problems with my matrices. Seems like this fixed it. It converts a D3DXMATRIX rotation matrix to a 3x3matrix for ODE:
dMatrix3 matODE; matODE[0] = m._13; matODE[1] = m._12; matODE[2] = m._11; matODE[3] = 0.0f; matODE[4] = m._23; matODE[5] = m._22; matODE[6] = m._21; matODE[7] = 0.0f; matODE[8] = m._33; matODE[9] = m._32; matODE[10] = m._31; matODE[11] = 0.0f;
The order x,y,z is swapped to z,y,x. I'm not sure if this is needed in every project, but thought I could share it.
Also, Si Brown was kind enough to make his source code available, at http://www.sjbrown.co.uk/buggy.html
I use DirectX, and it seems like ODE has switched to single-precision!
There's also an issue about Direct X autonomously changing the internal FPU accuracy, leading to inconsistent calculations. Direct3D by default changes the FPU to single precision mode at program startup and does not change it back to improve speed (This means that your double variables will behave like float). To disable this behaviour, pass the D3DCREATE_FPU_PRESERVE flag to the CreateDevice call. This might adversely affect D3D performance (not much though). Search the mailing list for details.
To create the device in the right way you could do it in the following way:
//pD3D is asumed to be a valid pointer to a IDirect3D9 structure
pD3D->CreateDevice( D3DADAPTER_DEFAULT , //Use? default graphics card
D3DDEVTYPE_HAL , /* Hardwareaccelerated?, can be also be
* D3DDEVTYPE_REF*/
hWnd, /* handle of the window */
/*your old value*/ | D3DCREATE_FPU_PRESERVE, /* ex: D3DCREATE_HARDWARE_VERTEXPROCESSING |
* D3DCREATE_FPU_PRESERVE */
&PresentationParameter? , /* where PresentationParameter? is a
* D3DPRESENT_PARAMETERS structure */
&pReturnedDeviceInterface?); /* where pReturnedDeviceInterface? is a pointer
* to a IDirect3DDevice9 */
How do I handle gravitation and action at a distance (for a 3D space simulation)?
You will need to compute the forces acting on each of your objects and apply them each frame.
ODE Internals
Why is dVector3 the same size as dVector4? Why is a dMatrix not 3x3?
For making it SIMD friendly. i.e 16 byte aligned (there is no SIMD code in there right now, but there may be in the future).
I have a matrix does dBodygetRotation return ABCDEFGHI or ADGBEHCFI ?
That depends on whether you consider yourself row vector, or column vector, convention.
The matrix is actually a 3x4 matrix, with the fourth values being undefined. Those four values live at offset 3, 7 and 11 when indexed as an array, and would contain the translation values if the matrix was a "real" 3x4.
If you consider yourself column vector on the right, it will return ABCxDEFyGHIz, which is row major,
| A B C |
M = | D E F |
| G H I |
which is the reverse of what you'd use in OpenGL (which is also column vector on the right).
If you consider yourself row vector on the left, it will return ADGxBEHyCFIz, which is column major, which is the reverse of what you'd use in DirectX (which is also row vector on the left).
Why are ODE's steps so crude?
When trying out ODE, I decided to test the accuracy of its solver over large steps. My test procedure was:
1. Create a world.
2. Create a body in the world.
3. Confirm that the body's position and linear velocity were 0,0,0.
4. Set the world's gravity to 0,0,-10
5. Step the world by 10.
6. Check the position and linear velocity of the body.
Now, as I did this, I ran the equations for this on pencil & paper next to me, and concluded:
New velocity: 0,0,-100 (Determined by gravity*timestep)
New position: 0,0,-500 (Determined by (gravity/2)*(timestep^2))
Checking ODE's results, I saw:
New velocity: 0,0,-100 (Good)
New position: 0,0,-1000 (Double what it should be)
I then verified my calculation by iterating it over 1000 steps of 0.01 and it came to roughly -500.
Next, I checked the source code to see what mechanism it used, and found ODE's internal step function was:
Vel += Force/Mass
Pos += Vel
When it could, more accurately, be:
Pos += ((Force/Mass)/2)*(Timestep^2) + Vel*Timestep
Vel += Force/Mass
Is there a reason that it uses its current method over this integral method?
Why does ODE have a random function? When does randomness ever have a place in physics simulations?
ODE with external Collision Detection Engines
NO ANSWER
And how does ODE compare to SOLID 3.5 (the version used in [Blender])?
NO ANSWER
From the Manual
How do I connect a body to the static environment with a joint?
Use dJointAttach with arguments (body,0) or (0,body).
Does ODE need or use graphics library X ?
No. ODE is a computational engine, and is completely independent of any graphics library. However the examples that come with ODE use OpenGL, and most interesting uses of ODE will need some graphics library to make the simulation visible to the user. But that's your problem.
Why do my rigid bodies bounce or penetrate on collision? My restitution is zero!
Sometimes when rigid bodies collide without restitution, they appear to inter-penetrate slightly and then get pushed apart so that they only just touch. The problem gets worse as the time step gets larger. What is going on?
The contact joint constraint is only applied after the collision is detected. If a fixed time step is being used, it is likely that the bodies have already penetrated when this happens. The error reduction mechanism will push the bodies apart, but this can take a few time steps (depending on the value of the ERP parameter).
This penetration and pushing apart sometimes makes the bodies look like they are bouncing, although it is completely independent of whether restitution is on or not.
Some other simulators have individual rigid bodies take variable sized timesteps to make sure bodies never penetrate much. However ODE takes fixed size steps, as automatically choosing a non-penetrating step size is problematic for an articulated rigid body simulator (the entire ARB structure must be stepped to account for the first penetration, which may result in very small steps).
There are three fixes for this problem:
- Take smaller time steps.
- Increase ERP to make the problem less visible.
- Do your own variable sized time stepping somehow.
How can an immovable body be created?
In other words, how can you create a body that doesn't move, but that interacts with other bodies? The answer is to create a geom only, without the corresponding rigid body object. The geom is associated with a rigid body ID of zero. Then in the contact callback when you detect a collision between two geoms with a nonzero body ID and a zero body ID, you can simply pass those two IDs to the dJointAttach function as normal. This will create a contact between the rigid body and the static environment.
Don't try to get the same effect by setting a very high mass/inertia on the "motionless" body and then resetting it's position/orientation on each time step. This can cause unexpected simulation errors.
Why would you ever want to set ERP less than one?
From the definition of the ERP value, it seems than setting it to one is the best approach, because then all joint errors will be fully corrected at each time step. However, ODE uses various approximations in its integrator, so ERP=1 will not usually fix 100% of the joint error. ERP=1 can work in some cases, but it can also result in instability in some systems. In these cases you have the option of reducing ERP to get a better behaving system.
Is it advisable to set body velocities directly, instead of applying a force or torque?
You should only set body velocities directly if you are setting the system to some initial configuration. If you are setting body velocities every time step (for example from motion capture data) then you are probably abusing your physical model, i.e. forcing the system to do what you want rather than letting it happen naturally.
The preferred method of setting body velocities during the simulation is to use joint motors. They can set body velocities to a desired value in one time step, provided that the force/torque limit is high enough.
Why, when I set a body's velocity directly, does it come up to speed slower when joined to other bodies?
What is likely happening is that you are setting the velocity of one body without also setting the velocity of the bodies that it is joined to. When you do this, you cause error in the system in subsequent time steps as the bodies come apart at their joints. The error reduction mechanism will eventually correct for this and pull the other bodies along, but it may take a few time steps and it will cause a noticeable "drag" on the original body.
Setting the velocity of a body will affect that body alone. If it is joined to other bodies, you must set the velocity of each one separately (and correctly) to prevent this behavior.
Should I scale my units to be around 1.0 ?
Say you need to simulate some behavior on the scale of a few millimeters and a few grams. These small lengths and masses will usually work in ODE with no problem. However occasionally you may experience stability problems that are caused by lack of precision in the factorizer. If this is the case, you can try scaling the lengths and masses in your system to be around 0.1..10. The time step should also be be scaled accordingly. The same guideline applies when large lengths and masses are being used.
In general, length and mass values around 0.1..1.0 are better as the factorizer may not lose so much precision. This guideline is especially helpful when single precision is being used.
I've made a car, but the wheels don't stay on properly!
If you are building a car simulation, typically you create a chassis body and attach four wheel bodies. However, you may discover that when you drive it around the wheels rotate in incorrect directions, as though the joint was somehow becoming ineffective. The problem is observed when the car is moving fast (so the wheels are rotating fast), and the car tries to turn a corner. The wheels appear to rotate off their proper constraints as though the "axles" had become bent. If the wheels are rotating slowly, or the turn is made slowly, the problem is less apparent.
The problem is that numerical errors are being caused by the high rotation speed of the wheels. Two functions are provided to fix this problem: dBodySetFiniteRotationMode and dBodySetFiniteRotationAxis. The wheel bodies should have their finite rotation mode set, and the wheel's finite rotation axes should be set every time step to match their hinge axes. This will hopefully fix most of the problem.
How do I make "one way" collision interaction
Suppose you need to have two bodies (A and B) collide. The motion of A should affect the motion of B as usual, but B should not influence A at all. This might be necessary, for example, if B is a physically simulated camera in a VR environment. The camera needs collision response so that it doesn't enter into any scene objects by mistake, but the motion of the camera should not affect the simulation. How can this be achieved?
To solve this, attach a contact joint between B and null (the world), then set the contact joint's motion fields to match A's velocities at the contact point. See the demo_motion.cpp sample distributed with ODE for an example.
The Windows version of ODE crashes with large systems
ODE with dWorldStep requires stack space roughly on the order of O(n)+O(m2), where n is the number of bodies and m is the sum of all the joint constraint dimensions. If m is large, this can be a lot of space!
Unix-like operating systems typically allocate stack space as it is needed, with an upper limit that might be in the hundreds of Mb. Windows compilers normally allocate a much smaller stack. If you experience crashes when running large systems, try increasing the stack size. For example, the MS VC++ command line compiler accepts the /Stack:num flag to set the upper limit.
Another option is to switch to dWorldQuickStep.
My simple rotating bodies are unstable!
If you have a box whose sides have different lengths, and you start it rotating in free space, you should observe that it just tumbles at the same speed forever. But sometimes in ODE the box will gain speed by itself, spinning faster and faster until it "explodes" (disappears off to infinity). Here is the explanation:
ODE uses a first order semi-implicit integrator. The "semi implicit" means that some forces are calculated as though an implicit integrator is being used, and other forces are calculated as though the integrator is explicit. The constraint forces (applied to bodies to keep the constraints together) are implicit, and the "external" forces (applied by the user, and due to rotational effects) are explicit. Now, inaccuracy in implicit integrators is manifested as a reduction in energy - in other words the integrator damps the system for you. Inaccuracy in explicit integrators has the opposite effect - it increases the system energy. This is why systems simulated with explicit first order integrators can explode.
So, a single body tumbling in space is effectively explicitly integrated. If the body's moments of inertia were equal (e.g. if it is a sphere) then the rotation axis will remain constant, and the integrator error will be small. If the body's moments of inertia are unequal then the rotation axis wobbles as momentum is transferred between different rotation directions. This is the correct physical behavior, but it results in higher integrator error. The integrator in this case is explicit so the error increases the energy, which causes faster and faster rotation, causing more and more error - leading to the explosion. The problem is particularly evident with long thin objects, where the 3 moments of inertia are highly unequal.
To prevent this, do one or more of the following:
- Make sure freely rotating bodies are dynamically symmetric (i.e. all moments of inertia are the same - the inertia matrix is a constant times the identity matrix). Note that you can still render and collide with a long thin box even though it has the inertia of a sphere.
- Make sure freely rotating bodies don't spin too fast (e.g. don't apply large torques, or supply extra damping forces).
- Add extra damping elements to the environment, e.g. don't use bouncy collisions that can reflect energy.
- Use smaller timesteps. This is bad for two reasons: it's slower, and ODE currently only has a first order integrator so the added accuracy is minimal.
- Use a higher order integrator. This is not yet an option in ODE.
In the future I may add a feature to ODE to modify the rotational dynamics of selected bodies so that they exhibit no rotational error with ODEs integrator.
My rolling bodies (e.g. wheels) sometimes get stuck between geoms
Consider a system where rolling bodies roll over an environment made up of multiple geometry objects. For example, this might be a car driving over a terrain (the rolling bodies are the wheels). If you find that the rolling bodies mysteriously come to a stop when they roll from one geometry object to another, or when they receive multiple contact points, then you may need to use a different contact friction model. This section explains the problem and the solution.
The Problem
An example of such a system is shown in figure 13, which shows a ball that has just rolled down a ramp and touched the ground.
Figure 13: A problem with rolling contact.
Normally, the ball should continue rolling along the ground, towards the right. However, if ODE's default contact friction mode is being used then the ball will come to a complete stop when it hits the ground. Why?
ODE has two ways to approximate friction: the default way (called the constant-force-limit approximation, or "box friction") and an improved way (called "friction pyramid approximation 1") which is obtained by setting the dContactApprox1 flag in the contact joint's surface mode field.
Consider the above picture. There are two contact points, one between the ball and the ramp, the other between the ball and the ground. If the box friction mode is used in both contacts and the mu parameter is set to dInfinity then the ball can not slip against the ramp or ground at either contact.
If no slip is possible at a ball contact point, then the center of the ball must move along a path that is an arc around the contact point. Thus the center of the ball is required to simultaneously move along the path "Arc 1" and "Arc 2". The only way to satisfy both paths at once is for the ball to stop moving altogether.
This is not a bug in ODE - so what is going on here? Objects in real life do not get stuck like this. The problem is that, in the simple "box" approximation of friction the tangential force available at a contact constraint to stop it slipping is independent of the normal force that prevents penetration. This is not real-life physics, so we should not be surprised that non-real-life motion results.
Note that this problem does not occur if mu is set to zero, but this is not a helpful solution because we need some amount of friction to model the real world.
The Solution
The solution is to use the dContactApprox1 flag in the contact's surface mode field, and set mu to some appropriate value between 0 and infinity. This mode ensures that there will only be a tangential anti-slipping force at the contact point if the contact normal force is nonzero. In the above example it turns out that contact-1 will have a zero normal force, so there will be no force applied at contact-1 at all, and the problem is solved! (the ball will roll along the ground properly.)
The dContactApprox1 mode may not be appropriate in all situations, which is why it is optional. It is important to remember that, although it is a better friction approximation, it is not true Coulomb friction. Thus it is still possible that you may encounter some examples of non-physical behavior.
How do i simulate "perfect" bounciness?
If I create 4 planes, and use the Plane2D Joint to restrict movement to the XY 2d plane, than add a box between the planes and give it a velocity, after 4-5 bounces it looses all its energy. I tried setting mu to zero and the surface.bounce parameter to 1, even setting soft_cfm to 1, but still the same results. I tried re-setting the velocity of the object every step like :
const dReal *speed = dyn_bodies[0].getLinearVel(); dReal len = sqrt(speed[0]*speed[0] + speed[1]*speed[1]); // speed_length dReal sx = speed[0] / len; // get a normalized speed_direction dReal sy = speed[0] / len; dyn_bodies[0].setLinearVel(sx*2, sy*2,0); // fix speed_vector length
...but than it would behave very unrealistically / strange. Also, no gravity is involved.
Known Issues
- When assigning a mass to a rigid body, the center of mass must be (0,0,0) relative to the body's position. But in fact this limitation has been in ODE from the start, so we can now regard it as a "feature" :)