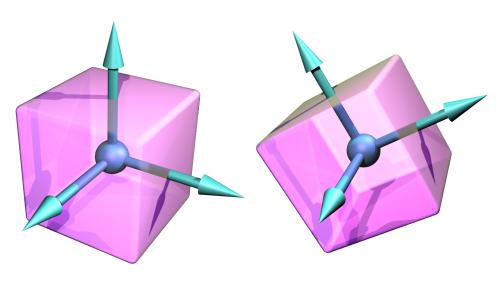
Figure 1: The body coordinate frame.
If ``rigid body simulation'' does not make much sense to you, check out What is a Physics SDK?.
This is the user guide for ODE version 0.5. Despite the low version number, ODE is reasonably mature and stable.
ODE is designed to be used in interactive or real-time simulation. It is particularly good for simulating moving objects in changeable virtual reality environments. This is because it is fast, robust and stable, and the user has complete freedom to change the structure of the system even while the simulation is running.
ODE uses a highly stable integrator, so that the simulation errors should not grow out of control. The physical meaning of this is that the simulated system should not "explode" for no reason (believe me, this happens a lot with other simulators if you are not careful). ODE emphasizes speed and stability over physical accuracy.
ODE has hard contacts. This means that a special non-penetration constraint is used whenever two bodies collide. The alternative, used in many other simulators, is to use virtual springs to represent contacts. This is difficult to do right and extremely error-prone.
ODE has a built-in collision detection system. However you can ignore it and do your own collision detection if you want to. The current collision primitives are sphere, box, capped cylinder, plane, ray, and triangular mesh - more collision objects will come later. ODE's collision system provides fast identification of potentially intersecting objects, through the concept of ``spaces''.
Here are the features:
This library is free software; you can redistribute it and/or modify it under the terms of EITHER:
Steps 2-4 (alternate): If you're on windows and using MSVC, you can use the workspace and project files in the VC6 subdirectory of the distribution.
Step 2: Get the GNU make tool. Many Unix platforms come with this, although sometimes it is called gmake. A version of GNU make for windows is available here.
Step 3: Edit the settings in the file config/user-settings. The list of supported platforms is given in that file.
Step 4: Run GNU make to configure and build ODE and the graphical test programs. The configuration process creates the file include/ode/config.h.
Step 5: To install the ODE library onto your system you should copy the lib/ and include/ directories to a suitable place, e.g. on Unix:
These are available from Apple. As of writing this can be found at: http://www.apple.com/macosx/x11. NOTE: there is a tiny link at the bottom right of the page for the SDK
Once the software is installed follow the normal build instructions.
Since ODE uses X11 you need to run the X11 server (which you should have installed, it's in the Applications Folder).
If you run the test app in the XTerm that the X11 server opens by default then they should run fine. If however you run them from a MacOS X Terminal then you need to define the environment variable DISPLAY. If DISPLAY is not defined then you will get a message saying: "cannot open X11 display".
For example to run the boxstack test you would type
cd ode/test
DISPLAY=:0.0 ./test_boxstack.exe
You can define this environment variable in your shell startup scripts
(for example in ~/.bashrc if you are using bash)#include <ode/ode.h>The ode directory in this statement is actually the include/ode directory of the ODE distribution. This header file will include others in the ode directory, so you need to set the include path of your compiler, e.g. in linux
gcc -c -I /home/username/ode/include myprogram.cpp

The origin of this coordinate frame is the body's point of reference. Some values in ODE (vectors, matrices etc) are relative to the body coordinate frame, and others are relative to the global coordinate frame.
Note that the shape of a rigid body is not a dynamical property (except insofar as it influences the various mass properties). It is only collision detection that cares about the detailed shape of the body.
Each island in the world is treated separately when the simulation step is taken. This is useful to know: if there are N similar islands in the simulation then the step computation time will be O(N).
Each body can be enabled or disabled. Disabled bodies are effectively ``turned off'' and are not updated during a simulation step. Disabling bodies is an effective way to save computation time when it is known that the bodies are motionless or otherwise irrelevant to the simulation.
If there are any enabled bodies in an island then every body in the island will be enabled at the next simulation step. Thus to effectively disable an island of bodies, every body in the island must be disabled. If a disabled island is touched by another enabled body then the entire island will be enabled, as a contact joint will join the enabled body to the island.

The first is a ball and socket joint that constraints the ``ball'' of one body to be in the same location as the ``socket'' of another body. The second is a hinge joint that constraints the two parts of the hinge to be in the same location and to line up along the hinge axle. The third is a slider joint that constraints the ``piston'' and ``socket'' to line up, and additionally constraints the two bodies to have the same orientation.
Each time the integrator takes a step all the joints are allowed to apply constraint forces to the bodies they affect. These forces are calculated such that the bodies move in such a way to preserve all the joint relationships.
Each joint has a number of parameters controlling its geometry. An example is the position of the ball-and-socket point for a ball-and-socket joint. The functions to set joint parameters all take global coordinates, not body-relative coordinates. A consequence of this is that the rigid bodies that a joint connects must be positioned correctly before the joint is attached.
This is most useful with contact joints, which are added and remove from the world in groups every time step.
There is a mechanism to reduce joint error: during each simulation step each joint applies a special force to bring its bodies back into correct alignment. This force is controlled by the error reduction parameter (ERP), which has a value between 0 and 1.
The ERP specifies what proportion of the joint error will be fixed during the next simulation step. If ERP=0 then no correcting force is applied and the bodies will eventually drift apart as the simulation proceeds. If ERP=1 then the simulation will attempt to fix all joint error during the next time step. However, setting ERP=1 is not recommended, as the joint error will not be completely fixed due to various internal approximations. A value of ERP=0.1 to 0.8 is recommended (0.2 is the default).
A global ERP value can be set that affects most joints in the simulation. However some joints have local ERP values that control various aspects of the joint.
Not all constraints are hard. Some ``soft'' constraints are designed to be violated. For example, the contact constraint that prevents colliding objects from penetrating is hard by default, so it acts as though the colliding surfaces are made of steel. But it can be made into a soft constraint to simulate softer materials, thereby allowing some natural penetration of the two objects when they are forced together.
There are two parameters that control the distinction between hard and soft constraints. The first is the error reduction parameter (ERP) that has already been introduced. The second is the constraint force mixing (CFM) value, that is described below.
Traditionally the constraint equation for every joint has the form
where v is a velocity vector for the bodies involved, J is a ``Jacobian'' matrix with one row for every degree of freedom the joint removes from the system, and c is a right hand side vector. At the next time step, a vector lambda is calculated (of the same size as c) such that the forces applied to the bodies to preserve the joint constraint are
ODE adds a new twist. ODE's constraint equation has the form
where CFM is a square diagonal matrix. CFM mixes the resulting constraint force in with the constraint that produces it. A nonzero (positive) value of CFM allows the original constraint equation to be violated by an amount proportional to CFM times the restoring force lambda that is needed to enforce the constraint. Solving for lambda gives
Thus CFM simply adds to the diagonal of the original system matrix. Using a positive value of CFM has the additional benefit of taking the system away from any singularity and thus improving the factorizer accuracy.
If CFM is set to zero, the constraint will be hard. If CFM is set to a positive value, it will be possible to violate the constraint by ``pushing on it'' (for example, for contact constraints by forcing the two contacting objects together). In other words the constraint will be soft, and the softness will increase as CFM increases. What is actually happening here is that the constraint is allowed to be violated by an amount proportional to CFM times the restoring force that is needed to enforce the constraint. Note that setting CFM to a negative value can have undesirable bad effects, such as instability. Don't do it.
By adjusting the values of ERP and CFM, you can achieve various effects. For example you can simulate springy constraints, where the two bodies oscillate as though connected by springs. Or you can simulate more spongy constraints, without the oscillation. In fact, ERP and CFM can be selected to have the same effect as any desired spring and damper constants. If you have a spring constant kp and damping constant kd, then the corresponding ODE constants are:
where h is the stepsize. These values will give the same effect as a spring-and-damper system simulated with implicit first order integration.
Increasing CFM, especially the global CFM, can reduce the numerical errors in the simulation. If the system is near-singular, then this can markedly increase stability. In fact, if the system is mis-behaving, one of the first things to try is to increase the global CFM.
Collisions between bodies or between bodies and the static environment are handled as follows:
The Coulomb friction model is a simple, but effective way to model friction at contact points. It is a simple relationship between the normal and tangential forces present at a contact point (see the contact joint section for a description of these forces). The rule is:
where fN and fT are the normal and tangential force vectors respectively, and mu is the friction coefficient (typically a number around 1.0). This equation defines a "friction cone" - imagine a cone with fN as the axis and the contact point as the vertex. If the total friction force vector is within the cone then the contact is in "sticking mode", and the friction force is enough to prevent the contacting surfaces from moving with respect to each other. If the force vector is on the surface of the cone then the contact is in "sliding mode", and the friction force is typically not large enough to prevent the contacting surfaces from sliding. The parameter mu thus specifies the maximum ratio of tangential to normal force.
ODE's friction models are approximations to the friction cone, for reasons of efficiency. There are currently two approximations to chose from:
and then proceeds to solve for the entire system with these fixed limits (in a manner similar to approximation 1 above). This differs from a true friction pyramid in that the "effective" mu is not quite fixed. This approximation is easier to use as mu is a unit-less ratio the same as the normal Coloumb friction coefficient, and thus can be set to a constant value around 1.0 without regard for the specific simulation.
[must describe what factors influence accuracy and stability].
The floating point data type is dReal. Other commonly used types are dVector3, dVector4, dMatrix3, dMatrix4, dQuaternion.
All 3-vector result arguments to get() function are pointers to arrays of dReal.
Larger vectors are always supplied and returned as pointers to arrays of dReal.
All coordinates are in the global frame except where otherwise specified.
All the objects in a world exist at the same point in time, thus one reason to use separate worlds is to simulate systems at different rates.
Most applications will only need one world.
This function is given the desired impulse as (ix,iy,iz)
and puts the force vector in force.
The current algorithm simply scales the impulse by 1/stepsize,
where stepsize is the step size for the next step that will
be taken. This function is given a dWorldID because, in the future, the force
computation may depend on integrator parameters that are set as
properties of the world.
For large systems this will use a lot of memory and can be very slow,
but this is currently the most accurate method.
For large systems this is a lot faster than dWorldStep,
but it is less accurate. QuickStep is great for stacks of objects especially when the auto-disable feature
is used as well.
However, it has poor accuracy for near-singular systems.
Near-singular systems can occur when using high-friction contacts, motors,
or certain articulated structures. For example, a robot with multiple legs
sitting on the ground may be near-singular. There are ways to help overcome QuickStep's inaccuracy problems:
Hmmm. dBodyGetRotation returns a 4x3 rotation matrix.
The ...RelForce and ...RelTorque functions take force vectors that are
relative to the body's own frame of reference. The ...ForceAtPos and ...ForceAtRelPos functions take an extra
position vector (in global or body-relative coordinates respectively)
that specifies the point at which the force is applied.
All other functions apply the force at the center of mass.
A disabled body that is connected through a joint to an enabled body will
be automatically re-enabled at the next simulation step. Disabled bodies do not consume CPU time, therefore to speed up the simulation
bodies should be disabled when they come to rest.
This can be done automatically with the auto-disable feature. If a body has its auto-disable flag turned on, it will automatically disable itself
when
Thus, every body has five auto-disable parameters: an enabled flag, a idle step count,
an idle time, and linear/angular velocity thresholds.
Newly created bodies get these parameters from world. The following functions set and get the enable/disable parameters of a body.
If this axis is zero (0,0,0), full finite rotations are performed on the body. If this axis is nonzero, the body is rotated by performing a partial finite
rotation along the axis direction followed by an infinitesimal rotation along
an orthogonal direction. This can be useful to alleviate certain sources of error caused by quickly
spinning bodies. For example, if a car wheel is rotating at high speed
you can call this function with the wheel's hinge axis as the argument to
try and improve its behavior.
Some joints, like hinge-2 need to be attached to two bodies to work.
If one of these returned body IDs is zero, the joint connects the other body
to the static environment.
If both body IDs are zero, the joint is in ``limbo'' and has no effect on
the simulation.
If this information is desired then the user can allocate a dJointFeedback
structure and pass its pointer to the dJointSetFeedback() function.
The feedback information structure is defined as follows: During the time step any feedback structures that are attached to joints will
be filled in with the joint's force and torque information.
The dJointGetFeedback() function returns the current feedback
structure pointer, or 0 if none is used (this is the default).
dJointSetFeedback() can be passed 0 to disable feedback for that joint. Now for some API design notes.
It might seem strange to require that users perform the allocation of
these structures. Why not just store the data statically in each
joint? The reason is that not all users will use the feedback
information, and even when it is used not all joints will need it.
It will waste memory to store it statically, especially as this
structure could grow to store a lot of extra information in the
future. Why not have ODE allocate the structure itself, at the user's request?
The reason is that contact joints (which are created and destroyed
every time step) would require a lot of time to be spent in memory
allocation if feedback is required. Letting the user do the allocation
means that a better allocation strategy can be provided, e.g simply
allocating them out of a fixed array. The alternative to this API is to have a joint-force callback. This
would work of course, but it has a few problems. First, callbacks tend
to pollute APIs and sometimes require the user to go through unnatural
contortions to get the data to the right place. Second, this would
expose ODE to being changed in the middle of a step (which
would have bad consequences), and there would have to be some kind of
guard against this or a debugging check for it - which would complicate
things.
When the hinge anchor or axis is set, the current position of the attached
bodies is examined and that position will be the zero angle.
When the axis is set, the current position of the attached bodies is
examined and that position will be the zero position.
A universal joint is like a ball and socket joint that constrains an
extra degree of rotational freedom. Given axis 1 on body 1, and axis 2
on body 2 that is perpendicular to axis 1, it keeps them
perpendicular. In other words, rotation of the two bodies about the
direction perpendicular to the two axes will be equal. In the picture, the two bodies are joined together by a cross. Axis 1
is attached to body 1, and axis 2 is attached to body 2. The cross
keeps these axes at 90 degrees, so if you grab body 1 and twist it,
body 2 will twist as well. A Universal joint is equivalent to a hinge-2 joint where the hinge-2's
axes are perpendicular to each other, and with a perfectly
rigid connection in place of the suspension. Universal joints show up in cars, where the engine causes a shaft, the
drive shaft, to rotate along its own axis. At some point you'd like to
change the direction of the shaft. The problem is, if you just bend
the shaft, then the part after the bend won't rotate about its own
axis. So if you cut it at the bend location and insert a universal
joint, you can use the constraint to force the second shaft to rotate
about the same angle as the first shaft. Another use of this joint is to attach the arms of a simple virtual
creature to its body. Imagine a person holding their arms straight
out. You may want the arm to be able to move up and down, and forward
and back, but not to rotate about its own axis. Here are the universal joint functions:
The hinge-2 joint is the same as two hinges connected in series, with
different hinge axes.
An example, shown in the above picture is the steering wheel of a car,
where one axis allows the wheel to be steered and the other axis allows
the wheel to rotate. The hinge-2 joint has an anchor point and two hinge axes.
Axis 1 is specified relative to body 1 (this would be the steering axis if
body 1 is the chassis).
Axis 2 is specified relative to body 2 (this would be the wheel axis if
body 2 is the wheel). Axis 1 can have joint limits and a motor, axis 2 can only have a motor. Axis 1 can function as a suspension axis, i.e. the constraint can be
compressible along that axis. The hinge-2 joint where axis1 is perpendicular to axis 2 is equivalent to
a universal joint with added suspension.
When the anchor or axis is set, the current position of the attached
bodies is examined and that position will be the zero angle.
The contact joint prevents body 1 and body 2 from inter-penetrating at the
contact point.
It does this by only allowing the bodies to have an ``outgoing'' velocity
in the direction of the contact normal.
Contact joints typically have a lifetime of one time step.
They are created and deleted in response to collision detection. Contact joints can simulate friction at the contact by applying special
forces in the two friction directions that are perpendicular to the
normal. When a contact joint is created, a dContact structure must be supplied.
This has the following definition:
fdir1 is a "first friction direction" vector that defines a direction
along which frictional force is applied.
It must be of unit length and perpendicular to the contact normal
(so it is typically tangential to the contact surface).
It should only be defined if the dContactFDir1 flag is set in
surface.mode.
The "second friction direction" is a vector computed to be perpendicular to
both the contact normal and fdir1. surface is a substructure that is set by the user.
Its members define the properties of the colliding surfaces.
It has the following members:
FDS is an effect that causes the contacting surfaces to side past each
other with a velocity that is proportional to the force that is
being applied tangentially to that surface. Consider a contact point where the coefficient of friction mu is
infinite. Normally, if a force f is applied to the two contacting
surfaces, to try and get them to slide past each other, they will not
move.
However, if the FDS coefficient is set to a positive value k
then the surfaces will slide past each other, building up to a
steady velocity of k*f relative to each other. Note that this is quite different from normal frictional effects:
the force does not cause a constant acceleration of the surfaces
relative to each other - it causes a brief acceleration to achieve the
steady velocity. This is useful for modeling some situations, in particular tires.
For example consider a car at rest on a road.
Pushing the car in its direction of travel will cause it to start
moving (i.e. the tires will start rolling).
Pushing the car in the perpendicular direction will have no effect, as
the tires do not roll in that direction.
However - if the car is moving at a velocity v, applying a force
f in the perpendicular direction will cause the tires to slip on
the road with a velocity proportional to f*v (Yes, this really
happens). To model this in ODE set the tire-road contact parameters as follows:
set friction direction 1 in the direction that the tire is rolling in,
and set the FDS slip coefficient in friction direction 2 to k*v,
where v is the tire rolling velocity and k is a tire parameter
that you can chose based on experimentation. Note that FDS is quite separate from the sticking/slipping effects of
Coulomb friction - both modes can be used together at a single contact
point.
The AMotor can be used in different modes.
In dAMotorUser mode, the user directly sets the axes that the AMotor
controls.
In dAMotorEuler mode, AMotor computes the euler angles
corresponding to the relative rotation, allowing euler angle torque motors
and stops to be set.
An AMotor joint with euler angles is shown in figure 10. In this diagram, a0, a1 and a2 are the three axes along
which angular motion is controlled.
The green axes (including a0) are anchored to body 1.
The blue axes (including a2) are anchored to body 2.
To get the body 2 axes from the body 1 axes the following sequence of
rotations is performed:
There is an important restriction when using euler angles: the theta 1
angle must not be allowed to get outside the range - pi /2 ... pi /2.
If this happens then the AMotor joint will become unstable (there is a
singularity at +/- pi /2).
Thus you must set the appropriate stops on axis number 1.
For dAMotorEuler mode:
For the parameter getting functions, if the system is out of alignment
(i.e. there is some joint error) then the anchor/axis values will be correct
with respect to body 1 only (or body 2 if you specified body 1 as zero in the
dJointAttach function). The default anchor for all joints is (0,0,0).
The default axis for all joints is (1,0,0). When an axis is set it will be normalized to unit length.
The adjusted axis is what the axis getting functions will return. When measuring a joint angle or position, a value of zero corresponds to the
initial position of the bodies relative to each other. Note that there are no functions to set joint angles or positions (or their
rates) directly, instead you must set the corresponding body positions and
velocities. This range of motion can be limited by setting stops on the joint.
The joint angle (or position) will be prevented from going below the
low stop value, or from going above the high stop value.
Note that a joint angle (or position) of zero corresponds to the
initial body positions. As well as stops, many joint types can have motors.
A motor applies a torque (or force) to a joint's degree(s) of freedom to
get it to pivot (or slide) at a desired speed.
Motors have force limits, which means they can apply no more than a
given maximum force/torque to the joint. Motors have two parameters: a desired speed, and the maximum force that is
available to reach that speed.
This is a very simple model of real life motors, engines or servos.
However, is it quite useful when modeling a motor (or engine or servo) that
is geared down with a gearbox before being connected to the joint.
Such devices are often controlled by setting a desired speed, and can only
generate a maximum amount of power to achieve that speed (which corresponds
to a certain amount of force available at the joint). Motors can also be used to accurately model dry (or Coulomb) friction in
joints.
Simply set the desired velocity to zero and set the maximum force to some
constant value - then all joint motion will be impeded by that force. The alternative to using joint stops and motors is to simply apply forces
to the affected bodies yourself.
Applying motor forces is easy, and joint stops can be emulated with
restraining spring forces.
However applying forces directly is often not a good approach and can lead
to severe stability problems if it is not done carefully. Consider the case of applying a force to a body to achieve a desired
velocity.
To calculate this force you use information about the current velocity,
something like this: This has several problems.
First, the parameter k must be tuned by hand.
If it is too low the body will take a long time to come up to speed.
If it is too high the simulation will become unstable.
Second, even if k is chosen well the body will still take a few time steps
to come up to speed.
Third, if any other ``external'' forces are being applied to the body, the
desired velocity may never even be reached (a more complicated force equation
would be needed, which would have extra parameters and its own problems). Joint motors solve all these problems: they bring the body up to speed
in one time step, provided that does not take more force than is allowed.
Joint motors need no extra parameters because they are actually implemented as
constraints.
They can effectively see one time step into the future to work out the correct
force.
This makes joint motors more computationally expensive than computing the
forces yourself, but they are much more robust and stable, and far less time
consuming to design with.
This is especially true with larger rigid body systems. Similar arguments apply to joint stops.
If a particular parameter is not implemented by a given joint, setting it
will have no effect. These parameter names can be optionally followed by a digit (2 or 3)
to indicate the second or third set of parameters, e.g. for the second axis
in a hinge-2 joint, or the third axis in an AMotor joint.
A constant dParamGroup is also defined such that:
dParamXi = dParamX + dParamGroup * (i-1)
ODE's dWorldStep function currently uses a "big matrix" method to
step the system. For some large systems this can be slow and can require
a lot of memory.
The StepFast1 algorithm provides an alternative way to step the system,
that sacrifices some accuracy for a big gain in speed and memory.
To use it, you simply call dWorldStepFast1 instead of
dWorldStep. The chart in figure 11 illustrates this speed advantage over the standard
dWorldStep algorithm. The graph relates the number of Degrees Of Freedom (DOFs) removed from a
system to the running time of the step. You may be able to tell that the
dWorldStep algorithm's running time is proportional to the cube of the
number of DOF's removed. The StepFast1 algorithm, however, is roughly
linear. So as islands increase in size (for example, when there is a large
pile-up of cars, a pile of "ragdoll corpses", or a wall of bricks) the
StepFast1 algorithm scales better than dWorldStep. All this means that
your application is more likely to keep a steady framerate, even in the
worst case scenario. The graph of DOFs removed to memory looks quite similar (see figure 12). dWorldStep requires memory proportional only to the square of the
number of DOF's removed. StepFast1, though, is still linear, but it has
nothing to do with the number of iterations per step. So this means the
dreaded "There was a big pile-up and ODE crashed without an error message"
problems (usually stack overflows) won't happen with StepFast1. Or at
least that you'll be rendering at a minute per frame or slower before
they do. The general answer to this question then, is: use StepFast1 when you don't
mind having a few more parameters to play with to get the system stable,
and you want to take advantage of it's speed or memory advantages. If you
find yourself running into situations in your simulation where large numbers
of bodies come in contact, and dWorldStep becomes too slow, try
switching to StepFast1. Many systems will work just fine with nothing more
than changing the dWorldStep function call to dWorldStepFast1.
Others will require a little tweaking to get them to work well with
StepFast1, usually in the masses of the bodies. When a joint connects two
bodies with a large mass ratio (i.e. one body has several times the mass
of the other body) StepFast1 may have trouble solving it. Another prospect for StepFast1 is designing for it from the ground up.
If you know you are going to build large worlds with many physically based
objects in them, then go ahead and plan to use StepFast1. Noting the mass
ratio problem above, you might want to consider making the mass of every
body in your system equal to 1.0. Or in a very small range, for example
between 0.5 and 1.5. Most of the other suggestions for speed and stability
apply to StepFast1, except that the object is no longer to remove as many
joints as possible from the equation. It can likely be shown that you will
get a better performance to stability ratio by spreading out mass among
several bodies connected by fixed joints rather than trying to implement
it as one massive body, especially if that one massive body means you have
to switch back to dWorldStep to keep things stable. A final prospect for StepFast1 is to use it only when you need to.
Since StepFast1 uses the body and world structures in exactly the same
way as dWorldStep, you can actually switch back and forth between the two
solvers at will. A good heuristic for when to make this switch is to
simply count contact joints while you are running the collision detection.
Since collision detection is normally called before the step, using this
method will ensure that the large island that would slow you down is never
sent to the dWorldStep solver (as opposed to waiting until after you've
already taken a step at 1 fps...). The only better solution would be a
hybrid island creation function, that sends small islands to dWorldStep,
and large islands to dWorldStepFast1. This may make it in the source at
some point in the future. Note that the functions pertaining to auto-disabling are not yet implemented!
Every rigid body also has a 3x3 rotation matrix that is derived from
the quaternion.
The rotation matrix and the quaternion always match. Some information about quaternions:
The following are utility functions for dealing with rotation matrices and
quaternions.
The following functions operate on this structure:
Using ODE's collision detection is optional - an alternative collision
detection system can be used as long as it can supply the right kinds
of contact information. depth is the depth to which the two bodies inter-penetrate each other.
If the depth is zero then the two bodies have a grazing contact, i.e. they
"only just" touch.
However, this is rare - the simulation is not perfectly accurate and will
often step the bodies too far so that the depth is nonzero. normal is a unit length vector that is, generally speaking,
perpendicular to the contact surface. g1 and g2 are the geometry objects that collided. The convention is that if body 1 is moved along the normal vector by a
distance depth (or equivalently if body 2 is moved the same distance in
the opposite direction) then the contact depth will be reduced to zero.
This means that the normal vector points "in" to body 1. In real life, contact between two bodies is a complex thing.
Representing contacts by contact points is only an approximation.
Contact "patches" or "surfaces" might be more physically accurate, but
representing these things in high speed simulation software is a challenge. Each extra contact point added to the simulation will slow it down some more,
so sometimes we are forced to ignore contact points in the interests of speed.
For example, when two boxes collide many contact points may be needed to
properly represent the geometry of the situation, but we may choose to
keep only the best three. Thus we are piling approximation on top of
approximation. Any geom can be collided against any other geom to yield zero or more
contact points. Spaces have the extra capability of being able to
collide their contained geoms together to yield internal contact
points. Geoms can be placeable or non-placeable. A placeable geom has a
position vector and a 3*3 rotation matrix, just like a rigid body,
that can be changed during the simulation.
A non-placeable geom does not have this capability - for example, it
may represent some static feature of the environment that can not be
moved. Spaces are non-placeable geoms, because each contained geom may
have its own position and orientation but it does not make sense for
the space itself to have a position and orientation. To use the collision engine in a rigid body simulation, placeable
geoms are associated with rigid body objects. This allows the
collision engine to get the position and orientation of the geoms from
the bodies. Note that geoms are distinct from rigid bodies in that a
geom has geometrical properties (size, shape, position and
orientation) but no dynamical properties (such as velocity or mass).
A body and a geom together represent all the properties of the
simulated object. Every geom is an instance of a class, such as sphere, plane, or
box. There are a number of built-in classes, described below, and you
can define your own classes as well. The point of reference of a placeable geoms is the point that is
controlled by its position vector. The point of reference for the
standard classes usually corresponds to the geom's center of
mass. This feature allows the standard classes to be easily connected
to dynamics bodies. If other points of reference are required, a
transformation object can be used to encapsulate a geom. The concepts and functions that apply to all geoms will be described
below, followed by the various geometry classes and the functions that
manipulate them. Space objects exist to make collision detection go faster.
Without spaces, you might generate contacts in your simulation by
calling dCollide to get contact points for every single
pair of geoms.
For N geoms this is O(N2) tests, which is too computationally
expensive if your environment has many objects. A better approach is to insert the geoms into a space and call
dSpaceCollide.
The space will then perform collision culling, which means
that it will quickly identify which pairs of geoms are potentially
intersecting.
Those pairs will be passed to a callback function, which can in turn
call dCollide on them.
This saves a lot of time that would have been spent in useless
dCollide tests, because the number of pairs passed to the
callback function will be a small fraction of every possible
object-object pair. Spaces can contain other spaces. This is useful for dividing a
collision environment into several hierarchies to further optimize
collision detection speed. This will be described in more detail
below.
When a space is destroyed, if its cleanup mode is 1 (the default) then
all the geoms in that space are automatically destroyed as well.
Setting a body ID of zero gives the geom its own position and
rotation, independent from any body. If the geom was previously connected
to a body then its new independent position/rotation is set to the current
position/rotation of the body. Calling these functions on a non-placeable geom results in a runtime
error in the debug build of ODE.
Calling these functions on a non-placeable geom results in a runtime
error in the debug build of ODE.
dGeomGetQuaternion copies the geom's quaternion into the space provided.
If the geom is attached to a body, the body's quaternion will be returned, i.e.
the resulting quaternion will be the same as the result of calling
dBodyGetQuaternion. Calling these functions on a non-placeable geom results in a runtime
error in the debug build of ODE.
This function may return a pre-computed cached bounding box, if it can
determine that the geom has not moved since the last time the bounding
box was computed.
User defined classes will return their own numbers.
dGeomIsEnabled() returns 1 if a geom is enabled or 0 if it is disabled.
New geoms are created in the enabled state.
The collision system has been designed to give the user maximum
flexibility to decide which objects will be tested against each other.
This is why are there are three collision functions instead of, for example,
one function that just generates all the contact points. Spaces may contain other spaces. These sub-spaces will typically
represent a collection of geoms (or other spaces) that are located
near each other.
This is useful for gaining extra collision performance by dividing the
collision world into hierarchies. Here is an example of where this is
useful: Suppose you have two cars driving over some terrain. Each car is made
up of many geoms. If all these geoms were inserted into the same
space, the collision computation time between the two cars would
always be proportional to the total number of geoms (or even to the
square of this number, depending on which space type is used). To speed up collision a separate space is created to represent each
car. The car geoms are inserted into the car-spaces, and the
car-spaces are inserted into the top level space. At each time step
dSpaceCollide is called for the top level space. This will do
a single intersection test between the car-spaces (actually between
their bounding boxes) and call the callback if they touch.
The callback can then test the geoms in the car-spaces against each
other using dSpaceCollide2. If the cars are not near each
other then the callback is not called and no time is wasted performing
unnecessary tests. If space hierarchies are being used then the callback function may be
called recursively, e.g. if dSpaceCollide calls the callback
which in turn calls dSpaceCollide with the same callback function.
In this case the user must make sure that the callback function is
properly reentrant. Here is a sample callback function that traverses through all spaces
and sub-spaces, generating all possible contact points for all
intersecting geoms: A space callback function is not allowed to modify a space while that
space is being processed with dSpaceCollide or
dSpaceCollide2. For example, you can not add or remove geoms
from a space, and you can not reposition the geoms within a space.
Doing so will trigger a runtime error in the debug build of ODE. Each bit position in the bitfield represents a different category of
object. The actual meaning of these categories (if any) is user defined.
The category bitfield indicates which categories a geom is a member of.
The collide bitfield indicates which categories the geom will collide with
during collision detection. A pair of geoms will be considered by dSpaceCollide and
dSpaceCollide2 for passing to the callback only if one of them
has a collide bit set that corresponds to a category bit in the other.
The exact test is as follows: Note that only dSpaceCollide and dSpaceCollide2 use
these bitfields, they are ignored by dCollide. Typically a geom will belong only to a single category, so only one bit will
be set in the category bitfield.
The bitfields are guaranteed to be at least 32 bits wide, so the user is
able to specify an arbitrary pattern of interactions for up to 32 objects.
If there are more than 32 objects then some of them will obviously have
to have the same category. Sometimes the category field will contain multiple bits set, e.g. if
the geom is a space them you may want to set the category to the union of
all the geom categories that are contained. Design note: Why don't we just have a single category bitfield and
use the test (cat1 & cat2) ? This is simpler, but a single field
requires more bits to represent some patterns of interaction.
For example, if 32 geoms have an interaction pattern that is a 5
dimensional hypercube, 80 bit are required in the simpler scheme.
The simpler scheme also makes it harder to determine what the
categories should be for some situations. flags specifies how contacts should be generated if the geoms touch.
The lower 16 bits of flags is an integer that specifies the maximum
number of contact points to generate.
Note that if this number is zero, this function just pretends that it
is one - in other words you can not ask for zero contacts.
All other bits in flags must be zero.
In the future the other bits may be used to select from different contact
generation strategies. contact points to an array of dContactGeom structures.
The array must be able to hold at least the maximum number of contacts.
These dContactGeom structures may be embedded within larger structures
in the array - the skip parameter is the byte offset from one
dContactGeom to the next in the array.
If skip is sizeof(dContactGeom) then contact points to a
normal (C-style) array.
It is an error for skip to be smaller than sizeof(dContactGeom). If the geoms intersect, this function returns the number of contact
points generated (and updates the contact array), otherwise it
returns 0 (and the contact array is not touched). If a space is passed as o1 or o2 then this function will collide
all objects contained in o1 with all objects contained in o2,
and return the resulting contact points.
This method for colliding spaces with geoms (or spaces with spaces) provides
no user control over the individual collisions.
To get that control, use dSpaceCollide or dSpaceCollide2
instead. If o1 and o2 are the same geom then this function will do
nothing and return 0. Technically speaking an object intersects with
itself, but it is not useful to find contact points in this case. This function does not care if o1 and o2 are in the same
space or not (or indeed if they are in any space at all).
The callback function can call dCollide on o1 and
o2 to generate contact points between each pair.
Then these contact points may be added to the simulation as contact
joints.
The user's callback function can of course chose not to call
dCollide for any pair, e.g. if the user decides that
those pairs should not interact. Other spaces that are contained within the colliding space are not
treated specially, i.e. they are not recursed into.
The callback function may be passed these contained spaces as one or
both geom arguments. dSpaceCollide() is guaranteed to pass all intersecting geom pairs
to the callback function, but it may also make mistakes and pass
non-intersecting pairs. The number of mistaken calls depends on the
internal algorithms used by the space.
Thus you should not expect that dCollide will return
contacts for every pair passed to the callback.
This function is similar to dSpaceCollide, except that it is
passed two geoms (or spaces) as arguments.
It calls the callback for all potentially intersecting pairs that contain
one geom from o1 and one geom from o2. The exact behavior depends on the types of o1 and o2:
Here are the functions used for spaces:
In dHashSpaceGetLevels the minimum and maximum levels are returned
through pointers. If a pointer is zero then it is ignored and no
argument is returned.
If any change is made to the space (including adding and deleting geoms)
then no guarantee can be made about how the index number of any particular
geom will change.
Thus no space changes should be made while enumerating the geoms. This function is guaranteed to be fastest when the geoms are accessed in
the order 0,1,2,etc. Other non-sequential orders may result in slower access,
depending on the internal implementation.
dWorldID dWorldCreate();
void dWorldDestroy (dWorldID);
void dWorldSetGravity (dWorldID, dReal x, dReal y, dReal z);
void dWorldGetGravity (dWorldID, dVector3 gravity);
void dWorldSetERP (dWorldID, dReal erp);
dReal dWorldGetERP (dWorldID);
void dWorldSetCFM (dWorldID, dReal cfm);
dReal dWorldGetCFM (dWorldID);
void dWorldSetAutoDisableFlag (dWorldID, int do_auto_disable);
int dWorldGetAutoDisableFlag (dWorldID);
void dWorldSetAutoDisableLinearThreshold (dWorldID, dReal linear_threshold);
dReal dWorldGetAutoDisableLinearThreshold (dWorldID);
void dWorldSetAutoDisableAngularThreshold (dWorldID, dReal angular_threshold);
dReal dWorldGetAutoDisableAngularThreshold (dWorldID);
void dWorldSetAutoDisableSteps (dWorldID, int steps);
int dWorldGetAutoDisableSteps (dWorldID);
void dWorldSetAutoDisableTime (dWorldID, dReal time);
dReal dWorldGetAutoDisableTime (dWorldID);
void dWorldImpulseToForce (dWorldID, dReal stepsize,
dReal ix, dReal iy, dReal iz, dVector3 force);
void dCloseODE();
5.1. Stepping Functions
void dWorldStep (dWorldID, dReal stepsize);
void dWorldQuickStep (dWorldID, dReal stepsize);
Increasing the number of QuickStep iterations may help a little bit, but
it is not going to help much if your system is really near singular.
void dWorldSetQuickStepNumIterations (dWorldID, int num);
int dWorldGetQuickStepNumIterations (dWorldID);
5.2. Contact Parameters
void dWorldSetContactMaxCorrectingVel (dWorldID, dReal vel);
dReal dWorldGetContactMaxCorrectingVel (dWorldID);
void dWorldSetContactSurfaceLayer (dWorldID, dReal depth);
dReal dWorldGetContactSurfaceLayer (dWorldID);
6. Rigid Body Functions
6.1. Creating and Destroying Bodies
dBodyID dBodyCreate (dWorldID);
void dBodyDestroy (dBodyID);
6.2. Position and orientation
void dBodySetPosition (dBodyID, dReal x, dReal y, dReal z);
void dBodySetRotation (dBodyID, const dMatrix3 R);
void dBodySetQuaternion (dBodyID, const dQuaternion q);
void dBodySetLinearVel (dBodyID, dReal x, dReal y, dReal z);
void dBodySetAngularVel (dBodyID, dReal x, dReal y, dReal z);
const dReal * dBodyGetPosition (dBodyID);
const dReal * dBodyGetRotation (dBodyID);
const dReal * dBodyGetQuaternion (dBodyID);
const dReal * dBodyGetLinearVel (dBodyID);
const dReal * dBodyGetAngularVel (dBodyID);
6.3. Mass and force
void dBodySetMass (dBodyID, const dMass *mass);
void dBodyGetMass (dBodyID, dMass *mass);
void dBodyAddForce (dBodyID, dReal fx, dReal fy, dReal fz);
void dBodyAddTorque (dBodyID, dReal fx, dReal fy, dReal fz);
void dBodyAddRelForce (dBodyID, dReal fx, dReal fy, dReal fz);
void dBodyAddRelTorque (dBodyID, dReal fx, dReal fy, dReal fz);
void dBodyAddForceAtPos (dBodyID, dReal fx, dReal fy, dReal fz,
dReal px, dReal py, dReal pz);
void dBodyAddForceAtRelPos (dBodyID, dReal fx, dReal fy, dReal fz,
dReal px, dReal py, dReal pz);
void dBodyAddRelForceAtPos (dBodyID, dReal fx, dReal fy, dReal fz,
dReal px, dReal py, dReal pz);
void dBodyAddRelForceAtRelPos (dBodyID, dReal fx, dReal fy, dReal fz,
dReal px, dReal py, dReal pz);
const dReal * dBodyGetForce (dBodyID);
const dReal * dBodyGetTorque (dBodyID);
void dBodySetForce (dBodyID b, dReal x, dReal y, dReal z);
void dBodySetTorque (dBodyID b, dReal x, dReal y, dReal z);
6.4. Utility
void dBodyGetRelPointPos (dBodyID, dReal px, dReal py, dReal pz,
dVector3 result);
void dBodyGetRelPointVel (dBodyID, dReal px, dReal py, dReal pz,
dVector3 result);
void dBodyGetPointVel (dBodyID, dReal px, dReal py, dReal pz,
dVector3 result);
void dBodyGetPosRelPoint (dBodyID, dReal px, dReal py, dReal pz,
dVector3 result);
void dBodyVectorToWorld (dBodyID, dReal px, dReal py, dReal pz,
dVector3 result);
void dBodyVectorFromWorld (dBodyID, dReal px, dReal py, dReal pz,
dVector3 result);
6.5. Automatic Enabling and Disabling
Every body can be enabled or disabled.
Enabled bodies participate in the simulation, while
disabled bodies are turned off and do not get updated during a simulation step.
New bodies are always created in the enabled state.
A body is considered to be idle when the magnitudes of both its linear velocity
and angular velocity are below given thresholds.
void dBodyEnable (dBodyID);
void dBodyDisable (dBodyID);
int dBodyIsEnabled (dBodyID);
void dBodySetAutoDisableFlag (dBodyID, int do_auto_disable);
int dBodyGetAutoDisableFlag (dBodyID);
void dBodySetAutoDisableLinearThreshold (dBodyID, dReal linear_threshold);
dReal dBodyGetAutoDisableLinearThreshold (dBodyID);
void dBodySetAutoDisableAngularThreshold (dBodyID, dReal angular_threshold);
dReal dBodyGetAutoDisableAngularThreshold (dBodyID);
void dBodySetAutoDisableSteps (dBodyID, int steps);
int dBodyGetAutoDisableSteps (dBodyID);
void dBodySetAutoDisableTime (dBodyID, dReal time);
dReal dBodyGetAutoDisableTime (dBodyID);
void dBodySetAutoDisableDefaults (dBodyID);
6.6. Miscellaneous Body Functions
void dBodySetData (dBodyID, void *data);
void *dBodyGetData (dBodyID);
void dBodySetFiniteRotationMode (dBodyID, int mode);
int dBodyGetFiniteRotationMode (dBodyID);
void dBodySetFiniteRotationAxis (dBodyID, dReal x, dReal y, dReal z);
void dBodyGetFiniteRotationAxis (dBodyID, dVector3 result);
int dBodyGetNumJoints (dBodyID b);
dJointID dBodyGetJoint (dBodyID, int index);
void dBodySetGravityMode (dBodyID b, int mode);
int dBodyGetGravityMode (dBodyID b);
7. Joint Types and Joint Functions
7.1. Creating and Destroying Joints
dJointID dJointCreateBall (dWorldID, dJointGroupID);
dJointID dJointCreateHinge (dWorldID, dJointGroupID);
dJointID dJointCreateSlider (dWorldID, dJointGroupID);
dJointID dJointCreateContact (dWorldID, dJointGroupID,
const dContact *);
dJointID dJointCreateUniversal (dWorldID, dJointGroupID);
dJointID dJointCreateHinge2 (dWorldID, dJointGroupID);
dJointID dJointCreateFixed (dWorldID, dJointGroupID);
dJointID dJointCreateAMotor (dWorldID, dJointGroupID);
void dJointDestroy (dJointID);
dJointGroupID dJointGroupCreate (int max_size);
void dJointGroupDestroy (dJointGroupID);
void dJointGroupEmpty (dJointGroupID);
7.2. Miscellaneous Joint Functions
void dJointAttach (dJointID, dBodyID body1, dBodyID body2);
void dJointSetData (dJointID, void *data);
void *dJointGetData (dJointID);
int dJointGetType (dJointID);
dJointTypeBall A ball-and-socket joint. dJointTypeHinge A hinge joint. dJointTypeSlider A slider joint. dJointTypeContact A contact joint. dJointTypeUniversal A universal joint. dJointTypeHinge2 A hinge-2 joint. dJointTypeFixed A fixed joint. dJointTypeAMotor An angular motor joint.
dBodyID dJointGetBody (dJointID, int index);
void dJointSetFeedback (dJointID, dJointFeedback *);
dJointFeedback *dJointGetFeedback (dJointID);
typedef struct dJointFeedback {
dVector3 f1; // force that joint applies to body 1
dVector3 t1; // torque that joint applies to body 1
dVector3 f2; // force that joint applies to body 2
dVector3 t2; // torque that joint applies to body 2
} dJointFeedback;
int dAreConnected (dBodyID, dBodyID);
int dAreConnectedExcluding (dBodyID, dBodyID, int joint_type);
7.3. Joint parameter setting functions
7.3.1. Ball and Socket
A ball and socket joint is shown in figure 4.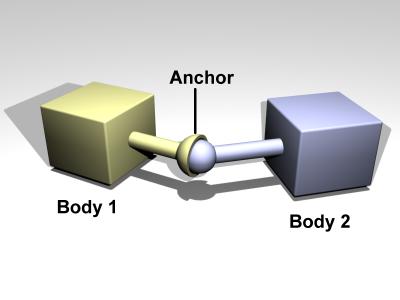
Figure 4: A ball and socket joint.
void dJointSetBallAnchor (dJointID, dReal x, dReal y, dReal z);
void dJointGetBallAnchor (dJointID, dVector3 result);
void dJointGetBallAnchor2 (dJointID, dVector3 result);
7.3.2. Hinge
A hinge joint is shown in figure 5.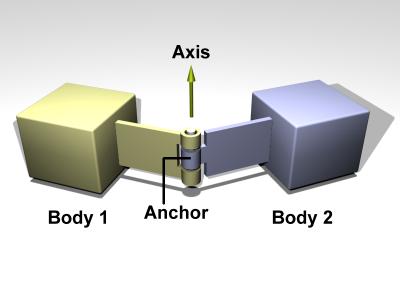
Figure 5: A hinge joint.
void dJointSetHingeAnchor (dJointID, dReal x, dReal y, dReal z);
void dJointSetHingeAxis (dJointID, dReal x, dReal y, dReal z);
void dJointGetHingeAnchor (dJointID, dVector3 result);
void dJointGetHingeAnchor2 (dJointID, dVector3 result);
void dJointGetHingeAxis (dJointID, dVector3 result);
dReal dJointGetHingeAngle (dJointID);
dReal dJointGetHingeAngleRate (dJointID);
7.3.3. Slider
A slider joint is shown in figure 6.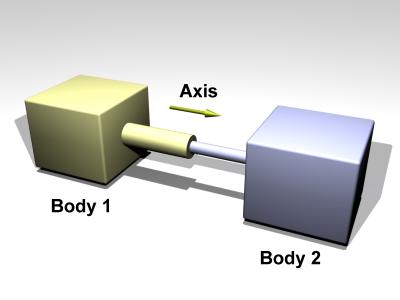
Figure 6: A slider joint.
void dJointSetSliderAxis (dJointID, dReal x, dReal y, dReal z);
void dJointGetSliderAxis (dJointID, dVector3 result);
dReal dJointGetSliderPosition (dJointID);
dReal dJointGetSliderPositionRate (dJointID);
7.3.4. Universal
A universal joint is shown in figure 7.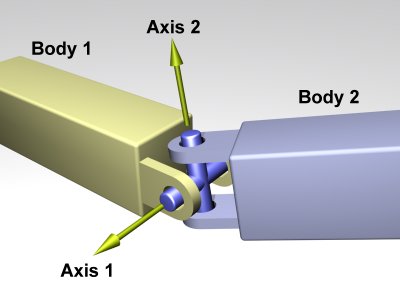
Figure 7: A universal joint.
void dJointSetUniversalAnchor (dJointID, dReal x, dReal y, dReal z);
void dJointSetUniversalAxis1 (dJointID, dReal x, dReal y, dReal z);
void dJointSetUniversalAxis2 (dJointID, dReal x, dReal y, dReal z);
void dJointGetUniversalAnchor (dJointID, dVector3 result);
void dJointGetUniversalAnchor2 (dJointID, dVector3 result);
void dJointGetUniversalAxis1 (dJointID, dVector3 result);
void dJointGetUniversalAxis2 (dJointID, dVector3 result);
7.3.5. Hinge-2
A hinge-2 joint is shown in figure 8.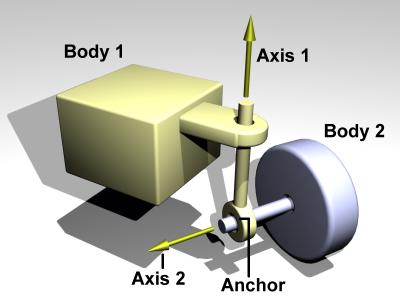
Figure 8: A hinge-2 joint.
void dJointSetHinge2Anchor (dJointID, dReal x, dReal y, dReal z);
void dJointSetHinge2Axis1 (dJointID, dReal x, dReal y, dReal z);
void dJointSetHinge2Axis2 (dJointID, dReal x, dReal y, dReal z);
void dJointGetHinge2Anchor (dJointID, dVector3 result);
void dJointGetHinge2Anchor2 (dJointID, dVector3 result);
void dJointGetHinge2Axis1 (dJointID, dVector3 result);
void dJointGetHinge2Axis2 (dJointID, dVector3 result);
dReal dJointGetHinge2Angle1 (dJointID);
dReal dJointGetHinge2Angle1Rate (dJointID);
dReal dJointGetHinge2Angle2Rate (dJointID);
7.3.6. Fixed
The fixed joint maintains a fixed relative position and orientation between
two bodies, or between a body and the static environment.
Using this joint is almost never a good idea in practice, except when
debugging.
If you need two bodies to be glued together it is better to represent that as
a single body.
void dJointSetFixed (dJointID);
7.3.7. Contact
A contact joint is shown in figure 9.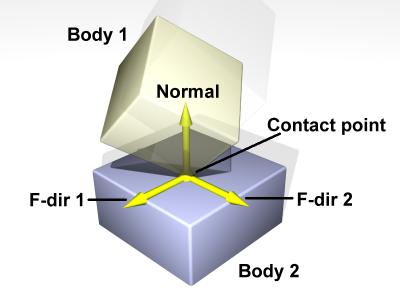
Figure 9: A contact joint.
struct dContact {
dSurfaceParameters surface;
dContactGeom geom;
dVector3 fdir1;
};
geom is a substructure that is set by the collision functions.
It is described in the collision section.
dContactMu2 If not set, use mu for both friction
directions. If set, use mu for friction direction 1,
use mu2 for friction direction 2. dContactFDir1 If set, take fdir1 as friction direction
1, otherwise automatically compute friction direction 1 to be
perpendicular to the contact normal (in which case its
resulting orientation is unpredictable). dContactBounce If set, the contact surface is bouncy,
in other words the bodies will bounce off each other.
The exact amount of bouncyness is controlled by the
bounce parameter. dContactSoftERP If set, the error reduction parameter of
the contact normal can be set with the soft_erp parameter.
This is useful to make surfaces soft. dContactSoftCFM If set, the constraint force mixing
parameter of the contact normal can be set with the
soft_cfm parameter. This is useful to make surfaces soft. dContactMotion1 If set, the contact surface is assumed to
be moving independently of the motion of the bodies.
This is kind of like a conveyor belt running over the surface.
When this flag is set, motion1 defines the surface
velocity in friction direction 1. dContactMotion2 The same thing as above, but for
friction direction 2. dContactSlip1 Force-dependent-slip (FDS) in friction
direction 1. dContactSlip2 Force-dependent-slip (FDS) in friction
direction 2. dContactApprox1_1 Use the friction pyramid approximation
for friction direction 1. If this is not specified then the
constant-force-limit approximation is used (and mu is a
force limit). dContactApprox1_2 Use the friction pyramid approximation
for friction direction 2. If this is not specified then the
constant-force-limit approximation is used (and mu is a
force limit). dContactApprox1 Equivalent to both dContactApprox1_1
and dContactApprox1_2. 7.3.8. Angular Motor
An angular motor (AMotor) allows the relative angular velocities of two
bodies to be controlled.
The angular velocity can be controlled on up to three axes, allowing
torque motors and stops to be set for rotation about those axes
(see the ``Stops and motor parameters'' section below).
This is mainly useful in conjunction will ball joints (which do not
constrain the angular degrees of freedom at all), but it can be used in
any situation where angular control is needed.
To use an AMotor with a ball joint, simply attach it to the same two bodies
that the ball joint is attached to.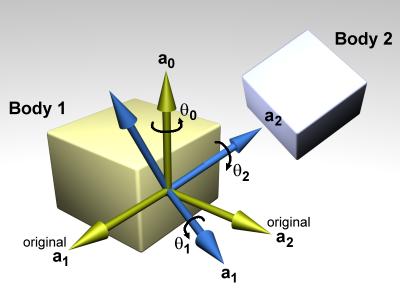
Figure 10: An AMotor joint with euler angles.
void dJointSetAMotorMode (dJointID, int mode);
int dJointGetAMotorMode (dJointID);
dAMotorUser The AMotor axes and joint angle settings are entirely
controlled by the user.
This is the default mode. dAMotorEuler Euler angles are automatically computed.
The axis a1 is also automatically computed.
The AMotor axes must be set correctly when in this mode,
as described below.
When this mode is initially set the current relative orientations
of the bodies will correspond to all euler angles at zero.
void dJointSetAMotorNumAxes (dJointID, int num);
int dJointGetAMotorNumAxes (dJointID);
void dJointSetAMotorAxis (dJointID, int anum, int rel,
dReal x, dReal y, dReal z);
void dJointGetAMotorAxis (dJointID, int anum, dVector3 result);
int dJointGetAMotorAxisRel (dJointID, int anum);
The axis vector (x,y,z) is always specified in global
coordinates regardless of the setting of rel.
There are two GetAMotorAxis functions, one to return the axis and one to
return the relative mode.
void dJointSetAMotorAngle (dJointID, int anum, dReal angle);
dReal dJointGetAMotorAngle (dJointID, int anum);
dReal dJointGetAMotorAngleRate (dJointID, int anum);
7.4. General
The joint geometry parameter setting functions should only be called after
the joint has been attached to bodies, and those bodies have been correctly
positioned, otherwise the joint may not be initialized correctly.
If the joint is not already attached, these functions will do nothing.7.5. Stop and motor parameters
When a joint is first created there is nothing to prevent it from
moving through its entire range of motion.
For example a hinge will be able to move through its entire angle,
and a slider will slide to any length.7.5.1. Parameter Functions
Here are the functions that set stop and motor parameters (as well as other
kinds of parameters) on a joint:
void dJointSetHingeParam (dJointID, int parameter, dReal value);
void dJointSetSliderParam (dJointID, int parameter, dReal value);
void dJointSetHinge2Param (dJointID, int parameter, dReal value);
void dJointSetUniversalParam (dJointID, int parameter, dReal value);
void dJointSetAMotorParam (dJointID, int parameter, dReal value);
dReal dJointGetHingeParam (dJointID, int parameter);
dReal dJointGetSliderParam (dJointID, int parameter);
dReal dJointGetHinge2Param (dJointID, int parameter);
dReal dJointGetUniversalParam (dJointID, int parameter);
dReal dJointGetAMotorParam (dJointID, int parameter);
dParamLoStop Low stop angle or position. Setting this to
-dInfinity (the default value) turns off the low stop.
For rotational joints, this stop must be greater than - pi to be
effective. dParamHiStop High stop angle or position. Setting this to
dInfinity (the default value) turns off the high stop.
For rotational joints, this stop must be less than pi to be
effective.
If the high stop is less than the low stop then both stops will
be ineffective. dParamVel Desired motor velocity (this will be an angular or
linear velocity). dParamFMax The maximum force or torque that the motor will use to
achieve the desired velocity.
This must always be greater than or equal to zero.
Setting this to zero (the default value) turns off the motor. dParamFudgeFactor The current joint stop/motor implementation has
a small problem:
when the joint is at one stop and the motor is set to move it away
from the stop, too much force may be applied for one time step,
causing a ``jumping'' motion.
This fudge factor is used to scale this excess force.
It should have a value between zero and one (the default value).
If the jumping motion is too visible in a joint, the value can be
reduced.
Making this value too small can prevent the motor from being able to
move the joint away from a stop. dParamBounce The bouncyness of the stops.
This is a restitution parameter in the range 0..1.
0 means the stops are not bouncy at all, 1 means maximum bouncyness. dParamCFM The constraint force mixing (CFM) value used when not
at a stop. dParamStopERP The error reduction parameter (ERP) used by the
stops. dParamStopCFM The constraint force mixing (CFM) value used by the
stops. Together with the ERP value this can be used to get spongy or
soft stops.
Note that this is intended for unpowered joints, it does not really
work as expected when a powered joint reaches its limit. dParamSuspensionERP Suspension error reduction parameter (ERP).
Currently this is only implemented on the hinge-2 joint. dParamSuspensionCFM Suspension constraint force mixing (CFM) value.
Currently this is only implemented on the hinge-2 joint. 7.6. Setting Joint Torques/Forces Directly
Motors (see above) allow you to set joint velocities directly. However, you
may instead wish to set the torque or force at a joint instead. These
functions do just that. Note that they don't affect the motor, but simply
call dBodyAddForce/dBodyAddTorque on the bodies attached to
it.
dJointAddHingeTorque(dJointID joint, dReal torque)
dJointAddUniversalTorques(dJointID joint, dReal torque1, dReal torque2)
dJointAddSliderForce(dJointID joint, dReal force)
dJointAddHinge2Torques(dJointID joint, dReal torque1, dReal torque2)
dJointAddAMotorTorques(dJointID joint, dReal torque0, dReal torque1,
dReal torque2)
8. StepFast
NOTE: The StepFast algorithm has been superseded by the QuickStep algorithm:
see the dWorldQuickStep function.
However, much of the following discussion also applies to QuickStep, except for
the details of the method used.
Figure 11: Speed advantage of StepFast.
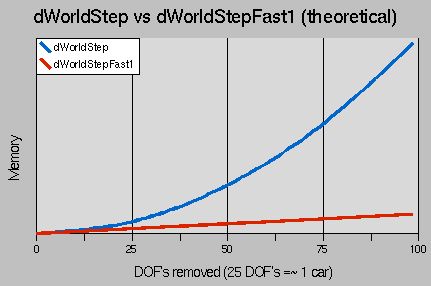
Figure 12: Memory advantage of StepFast.
8.1. When to use StepFast1
As shown above, StepFast1 is quite good when it comes to speed and memory
usage. All this power doesn't come for free, though; all optimizations are
a trade-off of one kind or another. I've already mentioned that StepFast1
trades off accuracy for it's speed and memory advantages. You actually get
to choose just how much accuracy you give away though, at the cost of speed,
by adjusting the number of iterations per step. Though you may never reach
the accuracy of dWorldStep (or you may surpass it, depending on the
type of inaccuracy), you can be almost certain that a larger number of
iterations will give you more accurate results (more slowly). So StepFast1
can be used in a good variety of situations.8.2. When NOT to use StepFast1
Though there are several specific situations when it as advisable not to
use StepFast1, I believe they can all be summed up in a single statement:
Don't use StepFast1 when accuracy is more important than speed or memory
to you. You may still want to evaluate it in this case and see if the
inaccuracies are even noticeable, perhaps with a relatively large number
of iterations (20+).8.3. How it works
For any interested parties out there, here's a quick rundown of how the
StepFast1 algorithm works. The general problem that ODE tries to solve
is a system of linear (in)equalities in (m = constraints) unknowns,
where one constraint constrains 1 Degree of Freedom in one joint.
For large islands of bodies with many joints between them, this can
take a rather large O(m2) array, which takes O(m3) time to solve.
StepFast1 completely avoids creating the large matrix by making an
assumption: at relatively small timesteps, the effect of any given joint
is so localized that it can be calculated without respect to any other
joint in the system, and any conflicting joints will cancel each other
out before the body actually moves. So StepFast1 uses the same solution
method (LCP) to solve the same problem, only localized to a single joint
(where m <= 6). It gets away with this by sub-dividing the timestep and
repeating the process over really small timesteps (i = maxiterations) times.
So the running time of StepFast1 is "roughly" O(m i). It's really closer
to O(j i (m/j)3) = O(m i (m/j)2), where j = joints, but (m/j)
is never > 6, so (m/j)2 is factored out as a constant.8.4. Experimental Utilities included with StepFast1
Several experimental functions have been added to ODE as part of the
StepFast1 flow of code, at least until they are validated. Most have to do
with the automatic disabling and enabling of bodies as yet another bit of
optimization. Here's the general idea:
8.5. API
void dWorldStepFast1(dWorldID, dReal stepsize, int maxiterations);
void dWorldSetAutoEnableDepthSF1(dWorldID, int autoEnableDepth);
int dWorldGetAutoEnableDepthSF1(dWorldID);
void dBodySetAutoDisableThresholdSF1(dBodyID, dReal autoDisableThreshold);
dReal dBodyGetAutoDisableThresholdSF1(dBodyID);
void dBodySetAutoDisableStepsSF1(dBodyID, int AutoDisableSteps);
int dBodyGetAutoDisableStepsSF1(dBodyID);
void dBodySetAutoDisableSF1(dBodyID, int doAutoDisable);
int dBodyGetAutoDisableSF1(dBodyID);
9. Support Functions
9.1. Rotation functions
Rigid body orientations are represented with quaternions.
A quaternion is four numbers [cos( theta /2),sin( theta /2)*u]
where theta is a rotation angle and u is a unit length rotation
axis.
void dRSetIdentity (dMatrix3 R);
void dRFromAxisAndAngle (dMatrix3 R,
dReal ax, dReal ay, dReal az, dReal angle);
void dRFromEulerAngles (dMatrix3 R,
dReal phi, dReal theta, dReal psi);
void dRFrom2Axes (dMatrix3 R, dReal ax, dReal ay, dReal az,
dReal bx, dReal by, dReal bz);
void dQSetIdentity (dQuaternion q);
void dQFromAxisAndAngle (dQuaternion q, dReal ax, dReal ay, dReal az,
dReal angle);
void dQMultiply0 (dQuaternion qa,
const dQuaternion qb, const dQuaternion qc);
void dQMultiply1 (dQuaternion qa,
const dQuaternion qb, const dQuaternion qc);
void dQMultiply2 (dQuaternion qa,
const dQuaternion qb, const dQuaternion qc);
void dQMultiply3 (dQuaternion qa,
const dQuaternion qb, const dQuaternion qc);
void dQtoR (const dQuaternion q, dMatrix3 R);
void dRtoQ (const dMatrix3 R, dQuaternion q);
void dWtoDQ (const dVector3 w, const dQuaternion q, dVector4 dq);
9.2. Mass functions
The mass parameters of a rigid body are described by a dMass structure:
typedef struct dMass {
dReal mass; // total mass of the rigid body
dVector4 c; // center of gravity position in body frame (x,y,z)
dMatrix3 I; // 3x3 inertia tensor in body frame, about POR
} dMass;
void dMassSetZero (dMass *);
void dMassSetParameters (dMass *, dReal themass,
dReal cgx, dReal cgy, dReal cgz,
dReal I11, dReal I22, dReal I33,
dReal I12, dReal I13, dReal I23);
[ I11 I12 I13 ]
[ I12 I22 I23 ]
[ I13 I23 I33 ]
void dMassSetSphere (dMass *, dReal density, dReal radius);
void dMassSetSphereTotal (dMass *, dReal total_mass, dReal radius);
void dMassSetCappedCylinder (dMass *, dReal density, int direction,
dReal radius, dReal length);
void dMassSetCappedCylinderTotal (dMass *, dReal total_mass,
int direction, dReal radius, dReal length);
void dMassSetCylinder (dMass *, dReal density, int direction,
dReal radius, dReal length);
void dMassSetCylinderTotal (dMass *, dReal total_mass, int direction,
dReal radius, dReal length);
void dMassSetBox (dMass *, dReal density,
dReal lx, dReal ly, dReal lz);
void dMassSetBoxTotal (dMass *, dReal total_mass,
dReal lx, dReal ly, dReal lz);
void dMassAdjust (dMass *, dReal newmass);
void dMassTranslate (dMass *, dReal x, dReal y, dReal z);
void dMassRotate (dMass *, const dMatrix3 R);
void dMassAdd (dMass *a, const dMass *b);
9.3. Math functions
[There are quite a lot of these, but they're not standardized enough to
document yet].9.4. Error and memory functions
[Document these later].10. Collision Detection
ODE has two main components: a dynamics simulation engine and a collision
detection engine.
The collision engine is given information about the shape of each
body. At each time step it figures out which bodies touch each other and
passes the resulting contact point information to the user.
The user in turn creates contact joints between bodies.10.1. Contact points
If two bodies touch, or if a body touches a static feature in its environment,
the contact is represented by one or more "contact points".
Each contact point has a corresponding dContactGeom structure:
struct dContactGeom {
dVector3 pos; // contact position
dVector3 normal; // normal vector
dReal depth; // penetration depth
dGeomID g1,g2; // the colliding geoms
};
pos records the contact position, in global coordinates.10.2. Geoms
Geometry objects (or ``geoms'' for short) are the fundamental objects
in the collision system. A geom can represents a single rigid shape
(such as a sphere or box), or it can represents a group of
other geoms - this is a special kind of geom called a ``space''.10.3. Spaces
A space is a non-placeable geom that can contain other geoms.
It is similar to the rigid body concept of the ``world'', except that
it applies to collision instead of dynamics.10.4. General geom functions
The following functions can be applied to any geom.
void dGeomDestroy (dGeomID);
void dGeomSetData (dGeomID, void *);
void *dGeomGetData (dGeomID);
void dGeomSetBody (dGeomID, dBodyID);
dBodyID dGeomGetBody (dGeomID);
void dGeomSetPosition (dGeomID, dReal x, dReal y, dReal z);
void dGeomSetRotation (dGeomID, const dMatrix3 R);
void dGeomSetQuaternion (dGeomID, const dQuaternion);
const dReal * dGeomGetPosition (dGeomID);
const dReal * dGeomGetRotation (dGeomID);
void dGeomGetQuaternion (dGeomID, dQuaternion result);
void dGeomGetAABB (dGeomID, dReal aabb[6]);
int dGeomIsSpace (dGeomID);
dSpaceID dGeomGetSpace (dGeomID);
int dGeomGetClass (dGeomID);
dSphereClass Sphere dBoxClass Box dCCylinderClass Capped cylinder dCylinderClass Regular flat-ended cylinder dPlaneClass Infinite plane (non-placeable) dGeomTransformClass Geometry transform dRayClass Ray dTriMeshClass Triangle mesh dSimpleSpaceClass Simple space dHashSpaceClass Hash table based space
void dGeomSetCategoryBits (dGeomID, unsigned long bits);
void dGeomSetCollideBits (dGeomID, unsigned long bits);
unsigned long dGeomGetCategoryBits (dGeomID);
unsigned long dGeomGetCollideBits (dGeomID);
void dGeomEnable (dGeomID);
void dGeomDisable (dGeomID);
int dGeomIsEnabled (dGeomID);
10.5. Collision detection
A collision detection ``world'' is created by making a space and then adding
geoms to that space.
At every time step we want to generate a list of contacts for all the geoms
that intersect each other.
Three functions are used to do this:
void nearCallback (void *data, dGeomID o1, dGeomID o2)
{
if (dGeomIsSpace (o1) || dGeomIsSpace (o2)) {
// colliding a space with something
dSpaceCollide2 (o1,o2,data,&nearCallback);
// collide all geoms internal to the space(s)
if (dGeomIsSpace (o1)) dSpaceCollide (o1,data,&nearCallback);
if (dGeomIsSpace (o2)) dSpaceCollide (o2,data,&nearCallback);
}
else {
// colliding two non-space geoms, so generate contact
// points between o1 and o2
int num_contact = dCollide (o1,o2,max_contacts,contact_array,skip);
// add these contact points to the simulation
...
}
}
...
// collide all objects together
dSpaceCollide (top_level_space,0,&nearCallback);10.5.1. Category and Collide Bitfields
Each geom has a ``category'' and ``collide'' bitfield that can be used
to assist the space algorithms in determining which geoms should
interact and which should not. Use of this feature is optional - by
default geoms are considered to be capable of colliding with any
other geom.
// test if geom o1 and geom o2 can collide
cat1 = dGeomGetCategoryBits (o1);
cat2 = dGeomGetCategoryBits (o2);
col1 = dGeomGetCollideBits (o1);
col2 = dGeomGetCollideBits (o2);
if ((cat1 & col2) || (cat2 & col1)) {
// call the callback with o1 and o2
}
else {
// do nothing, o1 and o2 do not collide
}10.5.2. Collision Detection Functions
int dCollide (dGeomID o1, dGeomID o2, int flags,
dContactGeom *contact, int skip);
void dSpaceCollide (dSpaceID space,
void *data, dNearCallback *callback);
typedef void dNearCallback (void *data, dGeomID o1, dGeomID o2);
The data argument is passed from dSpaceCollide directly
to the callback function. Its meaning is user defined.
The o1 and o2 arguments are the geoms that may be near
each other.
void dSpaceCollide2 (dGeomID o1, dGeomID o2,
void *data, dNearCallback *callback);
If this function is given a space and an geom X in that same space,
this case is not treated specially. In this case the callback will
always be called with the pair (X,X), because an objects always
intersects with itself.
The user may either test for this case and ignore it, or just pass the
pair (X,X) to dCollide (which will be guaranteed to return 0).
The strategy used may depends on a number of rules, but in general
the space with less objects has its geoms examined one-by-one.
10.6. Space functions
There are several kinds of spaces. Each kind uses different internal
data structures to store the geoms, and different algorithms to
perform the collision culling:
dSpaceID dSimpleSpaceCreate (dSpaceID space);
dSpaceID dHashSpaceCreate (dSpaceID space);
dSpaceID dQuadTreeSpaceCreate (dSpaceID space, dVector3 Center,
dVector3 Extents, int Depth);
void dSpaceDestroy (dSpaceID);
void dHashSpaceSetLevels (dSpaceID space, int minlevel, int maxlevel);
void dHashSpaceGetLevels (dSpaceID space, int *minlevel, int *maxlevel);
void dSpaceSetCleanup (dSpaceID space, int mode);
int dSpaceGetCleanup (dSpaceID space);
void dSpaceAdd (dSpaceID, dGeomID);
void dSpaceRemove (dSpaceID, dGeomID);
int dSpaceQuery (dSpaceID, dGeomID);
int dSpaceGetNumGeoms (dSpaceID);
dGeomID dSpaceGetGeom (dSpaceID, int i);
10.7. Geometry Classes
10.7.1. Sphere Class
dGeomID dCreateSphere (dSpaceID space, dReal radius);
void dGeomSphereSetRadius (dGeomID sphere, dReal radius);
dReal dGeomSphereGetRadius (dGeomID sphere);
dReal dGeomSpherePointDepth (dGeomID sphere, dReal x, dReal y, dReal z);
10.7.2. Box Class
dGeomID dCreateBox (dSpaceID space, dReal lx, dReal ly, dReal lz);
void dGeomBoxSetLengths (dGeomID box, dReal lx, dReal ly, dReal lz);
void dGeomBoxGetLengths (dGeomID box, dVector3 result);
dReal dGeomBoxPointDepth (dGeomID box, dReal x, dReal y, dReal z);
10.7.3. Plane Class
dGeomID dCreatePlane (dSpaceID space,
dReal a, dReal b, dReal c, dReal d);